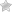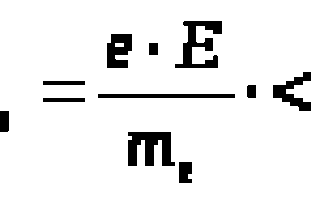Сохрани ссылку в одной из сетей:
Тема: Закон Ома в дифференциальной
форме
1. Постоянный электрический ток, его характеристики и условия существования.
;
2. Классическая электронная теория электропроводности (КЭТ) металлов и ее опытное обоснование. Плотность тока по КЭТ.
3. Вывод закона Ома в дифференциальной форме из электронных представлений.
4. Вывод закона Джоуля-Ленца
5. Затруднения классической теории электропроводности металлов.
1. Постоянный электрический ток, его характеристики и условия существования.
В электростатике речь шла о неподвижных электрических зарядах. На практике чаще приходится сталкиваться с движущимися зарядами. Явления (процессы) связанные с движением электрических зарядов изучаются в электродинамике.
- Всякое упорядоченное движение электрических зарядов называется электрическим током.
- Различают ток проводимости, ток в вакууме, конвекционный ток и ток смещения.
- Для появления и существования электрического тока необходимы следующие условия:
- 1. Наличие в данной среде электрического поля, энергия которого затрачивалась бы на перемещение зарядов;
- 2. Наличие в среде носителей электрического заряда, способных перемещаться в ней;
3. Электрическая цепь должна быть замкнутой.
Количественной характеристикой электрического тока служит сила тока. Силой тока называется скалярная физическая величина, численно равная количеству электрического заряда, переносимого через рассматриваемую поверхность за одну секунду.
. (1)
Сила тока имеет размерность и единицу измерения (Ампер).
(Следует отметить, что применение термина «сила» к величине, определяемой формулой (1) не является корректным. Более точное определение силе тока 1А будет дано позже.)
Электрический ток также характеризуется направлением. За направление тока принимается направление движения положительных зарядов.
Другой характеристикой электрического тока является плотность тока. Плотностью тока называется векторная физическая величина, совпадающая по направлению с направлением движения положительных зарядов и численно равная силе тока через единицу площади поперечного сечения проводника.
- ; , (2)
- где dI – сила тока через элементdS поперечного сечения проводника.
- При известном значении плотности тока, силу тока в проводнике можно определить следующей формулой
- , (3)
- где n – нормаль элемента dS.
Постоянным электрическим током называется ток, у которого не изменяются ни величина, ни направление. Опыты показывают, что плотность постоянного тока одинакова по всему поперечному сечению проводника. Поэтому для постоянного тока справедливы формулы
(4) и (5)
2. Классическая электронная теория электропроводности металлов (КЭТ) и ее опытное обоснование. Плотность тока по КЭТ.
Для выяснения природы носителей тока в металлах к началу XX века был проведен ряд опытов. Один из наиболее простых опытов был проведен немецким ученым Рикке К. (1901г.). В этом опыте через последовательно соединенные разнородные металлические (Cu-Al-Cu) проводники пропускался электрический ток в течение года.
Количество электрического заряда, прошедшего через проводники за это время, составило Q=3,5∙106 Кл. Исследование торцов проводников по окончанию опыта показало, что электрический ток не сопровождается переносом атомов.
На основании такого простого опыта был сделан важный вывод о том, что перенос электрического заряда в металлах не связан с переносом вещества и носители электрического тока во всех металлах одинаковы.
В опытах российских ученых Мандельштама Л.И. и Папалекси Н.Д. и американских ученых Толмена Р. и Стюарта Б. был измерен удельный заряд носителей тока.
Оказалось, что полученное значение удельного заряда очень близко к значению удельного заряда электрона, которое было измерено ранее.
Таким образом, было экспериментально доказано, что носителями электрического тока проводимости в металлах являются свободные электроны.
Немецким ученым Друде П., на основе представлений о свободных электронах, в начале XX века была создана классическая электронная теория электропроводности металлов.
В классической электронной теории электропроводности (КЭТ) металлов электроны проводимости (свободные электроны) рассматриваются как электронный газ, подчиняющийся законам идеального одноатомного газа.
Электроны проводимости, также как атомы газа, описываются законом Максвелла для их распределения по скоростям и энергиям теплового движения. При своем движении электроны сталкиваются с ионами (узлами кристаллической решетки). Поэтому им приписывается средняя длина свободного пробега.
Используя закон равнораспределения энергии по степеням свободы можно оценить среднюю скорость теплового движения электронов
(6) или
Как видим, значение средней скорости достаточно велико. Однако, тепловое движение электронов, вследствие своей хаотичности, не может привести к возникновению электрического тока (упорядоченного движения).
Если к концам проводника приложить разность потенциалов, то свободные электроны приобретут дополнительную скорость υЕ вдоль поля, которая, накладываясь на тепловую скорость, приведет к упорядоченному движению. Т.е. в проводнике возникнет электрический ток.
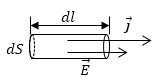
Получим выражение для плотности тока исходя из представлений об электронном газе. Для этого выделим отрезок проводника с поперечным сечением S и направим вектор напряженности Е электрического поля вдоль проводника. Свободные электроны приобретут некоторую среднюю скорость упорядоченного движения . За время dt площадку S пересекут все электроны, заключенные в объеме цилиндра с образующей ·dt.
Если число электронов в единице объема обозначить через n, а заряд электрона e, то за время dtчерез площадку S пройдет заряд
Тогда для плотности тока получим следующую формулу
Учитывая, что направление вектора плотности тока совпадает с направлением скорости, запишем формулу (8) в векторной форме
Оценка значения средней скорости упорядоченного движения электронов проводимости в меди, при предельно допустимом значении 107А·м2 плотности тока, дает величину ≈10-3 м·с-1.
Сравнивая полученное значение со значением средней скорости теплового движения электронов (формула 6) получим, что ≈108·. Т.е.
значение средней скорости теплового движения электронов на восемь! порядков превышает значение средней скорости их упорядоченного движения.
3. Вывод закона Ома в дифференциальной форме из электронных представлений.
Выведем формулу для плотности j тока, возникающего в металле по действием однородного электрического поля с напряженностью Е.
В электрическом поле на электроны будет действовать сила, определяемая формулой F=e·E. Т.е. движение электронов будет равноускоренным, с ускорением
(10).
Для упрощения расчетов положим, что все электроны имеют одно и то же значение средней скорости теплового движения и средней длины свободного пробега .
Положим также, что при каждом столкновении электрона с ионом кристаллической решетки он полностью теряет энергию, приобретенную в электрическом поле, и, после столкновения, начинает движение без начальной скорости. В этом случае график зависимости скорости упорядоченного движения υЕ электрона от времени будет иметь вид, показанный на рисунке.
Тогда к концу свободного пробега скорость упорядоченного движения электрона в среднем будет достигать значения
- где – среднее время свободного пробега.
- Среднее значение времени свободного пробега связано со средними значениями длины свободного пробега и результирующей скорости очевидным соотношением
- , (12)
- где υрезскладывается из скоростей теплового и упорядоченного движения .
В предыдущем вопросе было показано, что υТ>>υE, т.е. . Подставив последнее в формулу (12), а затем в формулу (11) получим для максимальной скорости
- . (13)
- Так как движение равноускоренное, то средняя скорость равна половине максимальной
- , (14)
- или =b·E, где (15) называется подвижностью носителей.
- Подставив формулу (15) в формулу (8) получим формулу для плотности тока
- , (16)
- или закона Ома в дифференциальной форме.
- В последней формуле произведение величин, стоящих перед величиной Е обозначается символом γ и называется удельной электропроводностью
- . (17)
Удельное сопротивление ρ обратно пропорционально удельной электропроводности ρ=1/γ. В формулу (17) входит средняя длина свободного пробега электронов, определяемая их столкновениями с ионами решетки.
Следовательно, в классической теории электропроводности наличие электрического сопротивления в металлах объясняется столкновениями свободных электронов с ионами решетки. С ростом температуры увеличивается скорость теплового движения электронов и интенсивность колебаний ионов решетки.
Это приводит к уменьшению и увеличению электрического сопротивления. Таким образом, формула (17) дает качественно правильную зависимость электрического сопротивления металлов от температуры.
- Учитывая формулу (17) и сонаправленность векторов j и E можно записать более компактно формулу (16) закона Ома в дифференциальной форме
- или . (18)
- Формула (18) позволяет вычислять плотность тока в точках, в которых известна напряженность электрического поля.
4. Вывод закона Джоуля-Ленца.
В конце свободного пробега каждый электрон передает иону решетки свою энергию, приобретенную в электрическом поле. Это приводит к нагреванию проводника. Среднее значение энергии, передаваемой каждым электроном иону, определяется формулой
- или, с учетом формулы (13), . (19)
- Умножив энергию, отдаваемую одним электроном (формула 19), на их концентрацию n и среднее число столкновений в единицу времени , получим формулу для удельной тепловой мощности w тока (энергии, выделяющейся в единице объема в единицу времени)
- . (20)
- Формула (20) позволяет вычислять удельную тепловую мощность тока в точках, в которых известна напряженность электрического поля и называется законом Джоуля-Ленца в дифференциальной форме.
5. Затруднения классической теории электропроводности металлов.
Классическая теория электропроводности (КЭТ), развитая Друде П., была весьма упрощенной. Например, предполагалось, что все электроны проводимости движутся с одинаковой скоростью. Поэтому ученый Лоренц Г.
, решив усовершенствовать КЭТ, применил к «электронному газу» закон Максвелла для распределения частиц по скоростям и получил парадоксальный результат. Оказалось, что уточненная КЭТ хуже согласуется с опытом, чем грубая теория Друдэ.
Таким образом, классическая теория электропроводности Друдэ-Лоренца столкнулась с весьма существенными затруднениями. Из них основными являются два:
1. Классическая теория электропроводности не смогла объяснить зависимость электрического сопротивления металлов от температуры.
Удельное сопротивление ρ обратно пропорционально электропроводности ρ=1/γ. Из формулы (17) следует, что ρ пропорционально средней скорости теплового движения , которая в свою очередь пропорциональна . Следовательно, при нагревании металлов их электрическое сопротивление теоретически должно возрастать пропорционально (ρ~).
Согласно же опыту, при нагревании металлов в широком интервале температур их электрическое сопротивление растет пропорционально температуре в первой степени (ρ~Т). КЭТ также не смогла объяснить открытое в 1911г. явление сверхпроводимости, проявляющееся в исчезновении электрического сопротивления при охлаждении металлов до сверхнизких температур.
2. Классическая теория электропроводности не смогла объяснить теплоемкость металлов.
По КЭТ теплоемкость металлов Смет складывается из теплоемкостей кристаллической решетки Среш и электронного газа Сгаз и, в случае одного моля, должна быть равна
Смет=3R+3/2R=37,5 Дж/(моль∙К).
Опыт же показывает, что значение теплоемкости металлов в соответствии с законом Дюлонга и Пти близко к 25 Дж/(моль∙К). Таким образом, обнаружилось неожиданное и непонятое с точки зрения КЭТ отсутствие теплоемкости у электронного газа.
Указанные затруднения КЭТ связаны с тем, что в ней не учитывается такое специфическое свойство электрона, как спин. (Спин – это собственный момент импульса микрочастицы). Спин электрона был открыт позже и был учтен в квантовой теории, которая устраняет все недостатки КЭТ и которая будет рассмотрена позже.
Вопросы для самопроверки:
1. Указать основные представления классической тории электропроводности металлов.
2. Как в КЭТ объясняется наличие электрического сопротивления? От чего зависит значение электрического сопротивления?
3. Вывести формулу закона Ома в дифференциальной форме.
4. Перечислить недостатки классической тории электропроводности металлов.
Источник: https://works.doklad.ru/view/EVZ0IgL7l2o.html
Закон ома в интегральной форме
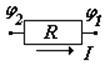
Закон Ома (в интегральной форме).[21]
|
j2 > j1 |
закон Ома для однородного участка цепи (без источника тока); смысл закона в том, что сила тока прямо пропорциональна разности потенциалов, приложенной к концам проводника | |
|
(·) |
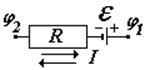
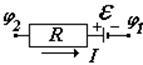
закон Ома для неоднородного участка цепи (с источником тока) (о выборе знаков см. дальше) | |
|
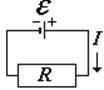
закон Ома для замкнутой цепи Во внешней цепи традиционно считается, что ток идет от «+» батареи к «-» |
||
|
| Напряжением U называется произведение силы тока на сопротивление участка. Из формулы (·) следует, что напряжение и разность потенциалов численно равны только для однородного участка цепи ( = 0). |
Перепишем (·), выразив разность потенциалов, т. к. вольтметр измеряет именно разность потенциалов, а не напряжение (они равны только для однородного участка): . Пусть требуется найти разность потенциалов Dj = j2 — j1. Выбрать знаки можно с помощью такого ненаучного правила: «Идем» по цепи от j2 к j1, если ток – с нами – берем «+», если упираемся в «+» батареи, — берем «+». Если при числовых расчетах получим, например, (-5 В) это означает, что j2 < j1.
- Вывод закона Ома на основе электронной теории электропроводности металлов.
- В электронной теории проводимости предполагается:
- 1) В металлах имеются свободные электроны, которые в отсутствие внешнего
- электрического поля движутся хаотически, а при
- наличии поля приобретают характер упорядоченного
движения (см. рис.).
- 2) Движение каждого электрона подчиняется законам
- классической механики.
- 3) Все вместе электроны образуют электронный газ и подчиняются законам
- молекулярной физики.
- 4) Взаимодействие электронов с ионами решетки рассматривается как простое
- столкновение, взаимодействием электронов между собой пренебрегается.
- 5) Напряженность поля внутри металла считается постоянной.
- 6) Все электроны под действием внешнего электрического поля приобретают
- одинаковые скорости vср.
При выводе закона Ома будем считать, что электрон, сталкиваясь с ионом, полностью отдает ему свою энергию, а затем снова набирает скорость под действием сил поля (см. рис.- фрагмент кристаллической решетки).
Электрон в кристалле участвует одновременно в двух движениях: хаотическом тепловом со скоростью u @ 105 м/с и направленном под действием поля со скоростью vср порядка 0,001 м/с, т. е.
u >> vср
| II закон Ньютона для электрона | |
| из кинематики, t – время движения электрона между двумя столкновениями | |
| средняя скорость электрона за время между двумя столкновениями | |
| l — средняя длина свободного пробега электрона – это расстояние, которое проходит электрон между двумя последовательными столкновениями с ионами (u >> vср) | |
| (··) | плотность тока в проводнике; подставив в эту формулу вышеприведенные, получим: |
|
мы получили закон Ома в дифференциальной форме, запишем его в векторном виде: |
| закон Ома в дифференциальной форме. В такой форме закон применим для бесконечно малого объема проводника, фактически – для точки проводника. | |
| (···) |
s — удельная электропроводность проводника; r — удельное сопротивление проводника |
Электронная теория проводимости металлов, несмотря на множество упрощающих предположений, позволяет теоретически вывести закон Ома и закон Джоуля – Ленца (см. ниже). Это свидетельствует о том, что модель поведения электронов в металле соответствует действительности. Вместе с тем эта теория столкнулась с рядом трудностей. Рассмотрим некоторые из них.
1)Теплоемкость металла теоретически должно складываться из теплоемкости кристаллической решетки и теплоемкости электронов: СМе = Среш +Сэлнов=
6R/2 + 3R/2 (для моля). Но из опыта следует, что теплоемкость почти всех твердых тел равна 3R. Таким образом, получается, что электроны не участвуют в теплоемкости, т. е.
не «принимают» тепло при нагревании вещества. В дальнейшем с развитием квантовой механики выяснилось, что электроны в металле могут иметь не любые энергии, а только те, значения которых лежат в разрешенных зонах (см.
III часть курса).
2)В формуле (···) e,m известны, n, u – можно вычислить, а s = 1/r измерить опытным путем. Таким образом можно оценить длину свободного пробега электрона l. Она оказалась равной порядка 10-5 см, тогда как расстояние между ионами примерно 10-8 см.
Получается, что электрон пролетает мимо сотен ионов, не сталкиваясь с ними. Это затруднение также объяснила квантовая механика: движение электрона в металле – это распространение некоторой волны, искажение этой волны происходит на примесях (чужеродных атомах), а их металле значительно меньше, чем атомов решетки.
Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/zakon-oma-v-integralnoj-forme
Закон Ома в интегральной форме
Для того, чтобы перейти к интегральной форме записи закона Ома для участка проводника, на котором действуют две силы, введем понятие линии тока.
Линия тока – кривая, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. В этом случае вектор плотности находится из соотношения:
Предположим, что удельное сопротивление (r) и напряженность поля движущих сил (E ⃗) на поперечном сечении проводника однородны, т.к. E ⃗ однородна, то j ⃗ так же однородная величина. Возьмем произвольное значение поперечного сечения цепи – S. Тогда:
, а значит
Последнее равенство до множим на dl (элементарное перемещение вдоль вектора плотности тока):
где
- dφ – элементарный сброс потенциала электростатического поля,
- dε – элементарная работа сторонних сил по перемещению единичного положительного заряда (ЭДС).
Отсюда:
Учитывая, что ρ/S dl=dR (элементарное сопротивление), запишем закон Ома в интегральной форме:
Закон Ома в интегральной форме для неоднородного участка цепи
Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:
где:
- – сопротивление участка,
- – работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,
- – работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),
- – абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).
Запишем значение напряжения при постоянном токе:
Отсюда запишем закон Ома:
Таким образом закон Ома в интегральной форме – это закон изменения механической энергии единичного положительного заряда на этом участке. В арифметическом виде этот закон можно записать так:
Решение задач
Какой будет плотность тока в металлическом проводнике с удельным сопротивлением ρ постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?
|
Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество, удельная проводимость которого изменяется в соответствии с линейным законом: в направлении перпендикулярном пластинам. Известно, что расстояние между пластинами – d, площадь пластин конденсатора – S. Каким будет ток через этот конденсатор, если напряжение на нем станет равно U?
|
|
Источник: https://zakon-oma.ru/v-integralnoj-forme.php
Закон Ома в дифференциальной и интегральной формах
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
I=
Однородным называется проводник, в котором не действуют сторонние силы. В этом случае, как мы видели, напряжение U совпадает с разностью потенциалов —, поддерживаемой на концах проводника. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит ом, равный сопротивлению такого проводника, в котором при напряжении в 1 в течет ток силой в 1 а.
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
R=
где l— длина проводника, S — площадь его поперечного сечения, — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если l=1 и S= 1, то R численно равно . В СИ измеряется в омо-метрах (ом-м)'. На практике часто характеризуют материал сопротивлением при l = 1 м и S = 1 мм2, т. е. выражают в (ом×мм2)/м.
Закон Ома можно записать в дифференциальной форме. Выделим мысленно в окрестности некоторой точки внутри проводника элементарный цилиндрический объем с образующими, параллельными вектору плотности тока j в данной точке. Через поперечное сечение цилиндра течет ток силой
jdS. Напряжение, приложенное к цилиндру, равно Edl где Е — напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле равно . Подставим эти значения в формулу тогда
jdS=×Edt
Носители заряда в каждой точке движутся в направлении вектора Е. Поэтому направления j и Е совпадают. Таким образом, можно написать
j=
где — величина, называемая коэффициентом электропроводности или просто проводимостью материала. Формула выражает закон Ома в дифференциальной форме.
Для любой точки внутри проводника напряженность результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил . Подставляя в формулу, получим
Умножим скалярно обе части на вектор , численно равный элементу длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока
- Так как скалярное произведение совпадающих по направлению векторов и , равно произведению их модулей, то это равенство можно переписать в виде
- С учетом
- Интегрируя по длине проводника от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем
Интеграл численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что
Таким образом,
где и — значение потенциала в т.1 и т.2.
Источник: https://students-library.com/library/read/94834-zakon-oma-v-differencialnoj-i-integralnoj-formah
Закон Ома ? для участка цепи, формула. Закон Ома ? в дифференциальной форме для полной цепи и её участка
Физический закон ома получен путём экспериментов. 3 формулировки ома – одни из основополагающих в физике, устанавливающие связь между электротоком, сопротивлением и энергонапряжением. Год открытия – 1826. Впервые все 3 физических закона ома сформулировал физик-экспериментатор немецкого происхождения Георг Ом, с фамилией которого связано их определение.
Мнемоническая схема
Согласно мнемосхеме, чтобы высчитать электросопротивление по закону ома для участка цепи постоянного тока, необходимо комплексное напряжение на участке цепи разделить на силу тока для полной цепи. Однако, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.
- Альтернативный способ вычислить токовое сопротивление по закону ома кратко подразумевает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.
- Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:
Применение на линии электропередач
В процессе доставки на линию электропередач потери энергии должны быть минимизированы. Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.
- Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.
- Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.
- Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.
Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.
Внимание!
Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.
Отображение в дифференциальной форме
- На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.
- Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.
- Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:
Интересно!
Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.
При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.
Переменный ток
- Величины являются комплексными, если речь идёт о синусоидальных формах энерготока с циклической частотой, в цепях которых присутствуют активная ёмкость с индуктивностью.
- В перечень комплексных величин входят:
- разность между потенциалами;
- сила тока;
- комплексное электросопротивление;
- модуль импеданса;
- разность индуктивного и ёмкостного сопротивлений;
- омическое электросопротивление;
- фаза импеданса.
Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и множество колебаний. Таким образом, можно сделать вывод о невозможности выполнения правила Ома для нелинейной электроцепи.
Внимание!
Гармоника – это колебание, частота которого кратна частоте напряжения.
Как трактуется правило Ома
Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.
Существует теория Друде, для выражения которой используются следующие величины:
- удельная электропроводимость;
- концентрированное размещение электронов;
- показатель элементарного заряда;
- время затихания по импульсам;
- эффективная масса электрона.
Внимание!
Все формулы Ома – первый, второй физический закон ома и третий распространяются на омические компоненты.
Перечень условий, при которых становится невозможным соблюдения правила Ома:
- высокие частоты с чрезмерно большой скоростью изменения электротока;
- пониженная температура сверхпроводимого вещества;
- перегрев проводника проходящим электротоком;
- в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
- в вакуумной или газонаполненной электролампе;
- для гетерогенного полупроводникового прибора;
- при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.
Интерпретация
Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.
Интересно!
Наиболее часто правило Ома применяется для металла и керамики.
Методы запоминания формулы
Чтобы легче запомнить формулу расчёта напряжения на участке цепи, следует выписать на бумажном листе все величины, из которых она состоит, в которую также входит сопротивление и сила тока. Искомую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет отображать действие, которое необходимо совершить для её вычисления.
Ниже будет представлено видео с подробным объяснением всех правил и формул, относящихся к рассматриваемой теме.
Закон Ома – один из самых несложных для понимания, который входит в программу школьных учебников физики начального уровня. Пользуясь графическим приёмом расчёта величин – при необходимости или для самопроверки, можно получить безошибочные результаты вычислений.
Источник: https://remont220.ru/osnovy-elektrotehniki/964-fizicheskiy-zakon-oma/
Обобщенный закон Ома в интегральной и дифференциальной формах
Обобщенный закон Ома в интегральной и дифференциальной формах.
- Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):
- где R – электрическое сопротивление проводника, определяющее упорядоченность перемещения свободных носителей тока.
Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит прежде всего от материала проводника, т.е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле
- Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры (по Цельсию):
- Для полной цепи, содержащей ЭДС, справедлив обобщенный закон Ома в интегральной форме
У чистых металлов α = 1/273 1/K
Для участка с источником тока и для участка с внешним сопротивлением будем иметь
Сложив, получим закон Ома для полной цепи
I(r+R)=ε
Разности потенциалов сократились, потому что работа электростатических сил по замкнутому контуру равна нулю. В случае многих источников направление тока заранее неизвестно; выбираем его произвольно и проходим контур в этом направлении. Записав соответствующие уравнения, получим
I∑Ri=∑±εi
Если сила тока окажется отрицательной, то направление тока надо изменить на противоположное.
Закон Ома в дифференциальной форме выражает связь между плотностью тока и напряженностью электростатического поля в бесконечно малом объеме проводника.
В проводнике носители заряда движутся в направлении действия силы (или электрического поля), т.е. вектор плотности тока и вектор напряженности поля коллинеарны.
Исходя из закона Ома, имеем:
А мы знаем, что или . Отсюда можно записать
это запись закона Ома в дифференциальной форме.
Источник: http://mini-fizik.blogspot.com/2016/06/blog-post_8.html
Дифференциальная форма закона Ома
Закон Ома в виде:
формулу для электросопротивления (R):
где $
ho $ — удельное сопротивление материала можно использовать для нахождения тока (I) в проводниках в тех случаях, если трубки тока являются цилиндрами с постоянным сечением ($S$). Довольно часто силу тока необходимо вычислить в проводящих средах с другими формами трубок тока.
Например, в сферическом конденсаторе, пространство между обкладками в котором заполнено проводящим материалом. В подобном случае формула расчета сопротивления (2) не применима, в связи с тем, что расстояние l различно для разных точек поверхности обкладок, площадь у каждой обкладки разная.
Следовательно, закон Ома необходимо представить в другой форме.
Переход от интегральной формы закона Ома к дифференциальной
Найдем связь между вектором плотности тока ($overrightarrow{j}$) и вектором напряженности электрического поля ($overrightarrow{E}$) в одной и той же точке проводящей среды.
Если вещество изотропно, то $overrightarrow{j}uparrow uparrow overrightarrow{E}$.
Выделим в окрестности рассматриваемой точки гипотетический цилиндр, образующие которого параллельны векторам напряженности поля и плотности тока (рис.1).
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
- Рис. 1
- Через поперечное сечение цилиндра (dS) (рис.1) течет ток, сила которого запишется как:
- Напряжение, приложенное к цилиндру можно выразить как:
- где $E$ — напряжённость поля в рассматриваемой точке. Сопротивление цилиндра получит выражение:
- Подставим формулы (3),(4),(5) в выражение (1), получим:
- Проведем сокращения, получим:
- Заменим удельное сопротивление ($
ho $), на удельную проводимость ($sigma $). Используем то, что векторы напряженности и плотности тока имеют одинаковые направления окончательно запишем:
Уравнение (8) называется законом Ома в дифференциальной форме. В отличие от закона Ома в интегральной форме (1) уравнение (8) содержит величины, которые характеризуют электрическое состояние среды в точке.
Напряженность поля, которая входит в уравнение (8) — это поле внутри проводящей среды при наличии тока.
Однако, если среда однородна, то в большинстве случаев это поле совпадает с электростатическим полем, то есть полем, которое было бы между электродами с таким же напряжением на них что и при наличии тока.
Следовательно, в однородном проводнике линии напряженности электростатического поля совпадают с линиями тока.
Дифференциальный закон Ома для анизотропных сред
В анизотропных средах для большинства электрических полей линейная связь между вектором плотности тока и вектором напряженности сохраняется. Однако удельная электрическая проводимость из скаляра переходит в тензор. В таком случае дифференциальный закон Ома выглядит следующим образом:
где индексы $ik$ пробегают значения x,y,z. Таким образом, тензор удельной проводимости имеет девять компонент из них шесть независимых. Тензор удельной проводимости симметричен:
При выборе осей координат, совпадающих с главными осями тензора, не равны нулю только 3 диагональные компоненты: ${sigma }_{xx}equiv {sigma }_1, {sigma }_{yy}equiv {sigma }_2, {sigma }_{zz}equiv {sigma }_3 $ — главные значения удельной электрической проводимости.
Пример 1
Задание: Найдите ток утечки через плоский конденсатор, если него подали напряжение U. Пространство между обкладками конденсатора заполнено веществом с удельным сопротивлением $
ho $и диэлектрической проницаемостью $varepsilon $. Емкость конденсатора равна C.
- Решение:
- За основу решения задачи возьмем закон Ома в дифференциальной форме:
- Силу тока, если бы мы знали плотность тока можно найти для данного случая, используя формулу:
- Напряженность поля между обкладками плоского конденсатора может быть найдена в соответствии с формулой:
[j=frac{1}{
ho }E left(1.1
ight).] [I=intlimits_S{jdS left(1.2
ight).}] [E=frac{U}{d}left(1.3
ight).]
Подставим закон Ома (1.1) в уравнение (1.2) и используем выражение (1.3):
[I=intlimits_S{frac{1}{
ho }frac{U}{d} dS=frac{1}{
ho }frac{U}{d} S left(1.4
ight).}]
- Емкость конденсатора связана с его геометрическими параметрами и веществом, которое заполняет пространство между обкладками:
- Используем полученное отношение $frac{S}{d}$ подставим в (1.4), получим:
- Ответ: Ток утечки равен $I=frac{1}{
ho }frac{U}{d} frac{C}{varepsilon {varepsilon }_0}$.
[C=frac{varepsilon {varepsilon }_0S}{d} o frac{S}{d}=frac{C}{varepsilon {varepsilon }_0}left(1.5
ight).] [I=frac{1}{
ho }frac{U}{d} frac{C}{varepsilon {varepsilon }_0}.]
Пример 2
Задание: Сравните напряженности электрического поля для сечений $S_1$ и $S_2$ (рис.2). Если по проводнику течет постоянный ток ($I=const$).
- Рис. 2
- Решение:
- Для решения используем закон Ома в дифференциальной форме:
- Будем считать, что проводник изотропный, запишем (2.1) в скалярном виде:
- При этом плотность силы тока можно записать как:
[overrightarrow{j}=sigma overrightarrow{E }left(2.1
ight).] [j=sigma E left(2.2
ight).] [j=frac{I}{S}left(2.3
ight).]
Подставим (2.3) в (2.2), получим:
[frac{I}{S}=уEleft(2.4
ight).]
Следовательно,
[E=frac{I}{sigma S}left(2.5
ight).]
Мы получили, что при $I=const, sigma =const$. Напряженность поля зависит только от площади поперечного сечения проводника, причем $Esim frac{1}{S}.$
Ответ: Так как $Esim frac{1}{S}$, то $E_2left(S_2
ight)
Источник: https://spravochnick.ru/fizika/postoyannyy_elektricheskiy_tok/differencialnaya_forma_zakona_oma/
17.4. Закон Ома в интегральной форме
Для любой точки внутри проводника напряженность результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил . Подставляя в (17.6), получим
Умножим скалярно обе части на вектор , численно равный элементу длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока
Так как скалярное произведение совпадающих по направлению векторов и , равно произведению их модулей, то это равенство можно переписать в виде
Интегрируя по длине проводника от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем
| (17.7) |
- Интеграл численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что
- Таким образом,
- Интеграл, содержащий вектор напряженности поля, сторонних сил, представляет собой эдс , действующей на участке 1-2
где и — значение потенциала в т.1 и т.2.
| (17.9) |
Интеграл
| (17.10) |
равен сопротивлению участка цепи 1-2.
Подставляя (17.10), (17.9) и (17.8) в (17.7), окончательно получим
| (17.11) |
Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической энергии, включённых на участке.
При замкнутой внешней цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей внешней цепи где или Отсюда
| (17.12) |
Источник: https://physics-lectures.ru/postoyannyj-elektricheskij-tok/17-4-zakon-oma-v-integralnoj-forme/
Закон Ома для однородного проводника. Закон Ома в дифференциальной форме
Закон Ома для однородного участка цепи (не содержащего источник тока) (интегральная форма закона Ома): сила тока /, текущего по однородному металлическому проводнику, пропорциональна напряжению U на конце проводника:
где R — электрическое сопротивление проводника.
Единица сопротивления в СИ — ом (Ом). 1 Ом — это сопротивление такого проводника, в котором течет постоянный ток 1 А при напряжении 1 В на его концах.
Сопротивление проводника зависит от его размеров и формы, а также от материала, из которого он изготовлен. Для однородного цилиндрического проводника сопротивление определяется как
- где / — длина проводника; S — площадь его поперечного сечения; р — удельное электрическое сопротивление, характеризующее материал проводника.
- Единица удельного электрического сопротивления в СИ — ом-метр (Ом • м).
- Для большинства металлов при не слишком низких температурах
Величина, обратная удельному электрическому сопротивлению, называется удельной электрической проводимостью вещества проводника:
Единица удельной электрической проводимости в СИ — сименс на метр (См/м).
Найдем связь между плотностью тока j и полем Е в одной и той же точке проводящей среды. Рассмотрим изотропный проводников котором направления векторов j и Е совпадают.
Рис. 14.1. К выводу локального закона Ома
Мысленно выделим в окрестности некоторой точки проводящей среды элементарный цилиндрический объем с_ образующими, параллельными вектору у, а следовательно, и вектору Е (рис. 14.1). Пусть dS — поперечное сечение цилиндра, (11 — его длина. В проводнике напряженность электрического поля E = Uldl.
Тогда из формул (14.11) и (14.12) для такого элементарного цилиндра получаем
- Ecll
- Следовательно, jdS = —,, .
- pdl/dS
Выражение (14.15) называется законом Ома в дифференциальной форме
(локальным законом Ома) и устанавливает связь между плотностью тока и напряженностью электрического поля в одной и той же точке пространства.
Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. Избыточный заряд может появиться только на поверхности однородного проводника в местах соприкосновения с другими проводниками или на участках, где проводник имеет неоднородности.
Отметим, что электростатическое поле внутри проводников при равновесии зарядов равно нулю. Поскольку в случае стационарных токов заряды^ возбуждающие электрическое поле, движутся, то электрическое поле Е стационарных токов существует и внутри проводников с током.
Источник: https://studref.com/504883/matematika_himiya_fizik/zakon_odnorodnogo_provodnika_zakon_differentsialnoy_forme

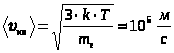
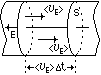 олучим выражение для плотности тока исходя из представлений об электронном газе. Для этого выделим отрезок проводника с поперечным сечением S и направим вектор напряженности Е электрического поля вдоль проводника. Свободные электроны приобретут некоторую среднюю скорость упорядоченного движения . За время dt площадку S пересекут все электроны, заключенные в объеме цилиндра с образующей ·dt.
олучим выражение для плотности тока исходя из представлений об электронном газе. Для этого выделим отрезок проводника с поперечным сечением S и направим вектор напряженности Е электрического поля вдоль проводника. Свободные электроны приобретут некоторую среднюю скорость упорядоченного движения . За время dt площадку S пересекут все электроны, заключенные в объеме цилиндра с образующей ·dt.