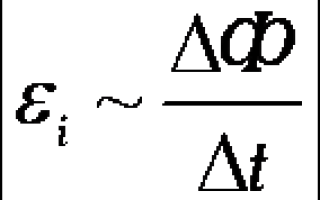Магнитный поток и электромагнитная индукция: физические формулы

Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем.

Основной закон электромагнитной индукции

Основной формулой, при помощи которой определяют ЭДС индукции (), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея).

В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает рассматриваемый контур:

   

где – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.

При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как:

   

Формулы ЭДС индукции для частных случаев

• ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как:
•    
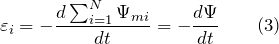
• где – потокосцепление.
• Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная:
•    
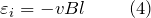
• где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
• Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна:
•    
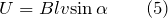
• где – угол между направлениями векторов и .
• При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как:
•    

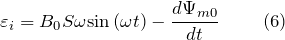
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля .

1. Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то:
2.    
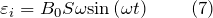
3. Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как:
4.    

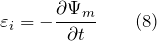
Примеры решения задач по теме «Электромагнитная индукция»

Понравился сайт? Расскажи друзьям!

Источник: https://ru.solverbook.com/spravochnik/formuly-po-fizike/formuly-elektromagnitnoj-indukcii/

Электромагнитная индукция. Магнитный поток — Класс!ная физика

«Физика — 11 класс»

Электромагнитная индукция

Английский физик Майкл Фарадей был уверен в единой природе электрических и магнитных явлений. Изменяющееся во времени магнитное поле порождает электрическое поле, а изменяющееся электрическое поле — магнитное.

• В 1831 году Фарадей открыл явление электромагнитной индукции, легшее в основу устройства генераторов, превращающих механическую энергию в энергию электрического тока.
• Явление электромагнитной индукции
• Явление электромагнитной индукции — это возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.
• Для своих многочисленных опытов Фарадей использовал две катушки, магнит, выключатель, источник постоянного тока и гальванометр.

Электрический ток способен намагнитить кусок железа. Не может ли магнит вызвать появление электрического тока?

В результате опытов Фарадей установил главные особенности явления электромагнитной индукции:

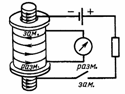
1). индукционный ток возникает в одной из катушек в момент замыкания или размыкания электрической цепи другой катушки, неподвижной относительно первой.

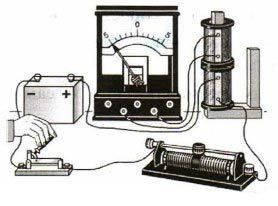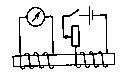
2). индукционный ток возникает при изменении силы тока в одной из катушек с помощью реостата 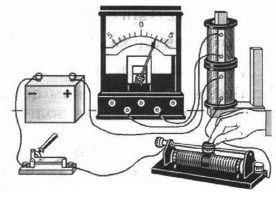3). индукционный ток возникает при движении катушек относительно друг друга 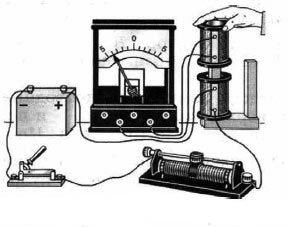4). индукционный ток возникает при движении постоянного магнита относительно катушки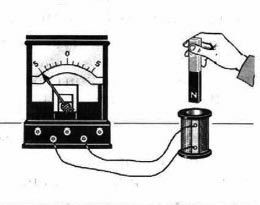

Вывод:

В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. И чем быстрее меняется число линий магнитной индукции, тем больше возникающий индукционный ток.

При этом не важно. что является причиной изменения числа линий магнитной индукции. Это может быть и изменение числа линий магнитной индукции, пронизывающих поверхность, ограниченную неподвижным проводящим контуром, вследствие изменения силы тока в соседней катушке,

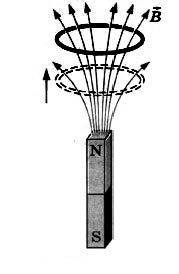
и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве, и т.д.

Магнитный поток — это характеристика магнитного поля, которая зависит от вектора магнитной индукции во всех точках поверхности, ограниченной плоским замкнутым контуром.

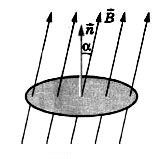
Есть плоский замкнутый проводник (контур), ограничивающий поверхность площадью S и помещенный в однородное магнитное поле. Нормаль (вектор, модуль которого равен единице) к плоскости проводника составляет угол α с направлением вектора магнитной индукции .

1. Магнитным потоком Ф (потоком вектора магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла α между векторами и :
2. Ф = BScos α
3. где Вcos α = Вn — проекция вектора магнитной индукции на нормаль к плоскости контура. Поэтому
4. Ф = BnS
5. Магнитный поток тем больше, чем больше Вn и S.
6. Магнитный поток зависит от ориентации поверхности, которую пронизывает магнитное поле.
7. Магнитный поток графически можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единицей магнитного потока является вебер. Магнитный поток в 1 вебер (1 Вб) создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Следующая страница «Направление индукционного тока. Правило Ленца» Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

Источник: https://class-fizika.ru/11_7.html

Магнитный поток (Ерюткин Е.С.). Видеоурок. Физика 9 Класс

Продолжая изучение темы «Электромагнитная индукция» давайте  подробнее остановиться на таком понятии, как магнитный поток.

Вы уже знаете, как обнаружить явление электромагнитной индукции — если замкнутый проводник пересекают магнитные линии, в этом проводнике возникает электрический ток. Такой ток называется индукционным.

• Теперь давайте обсудим, за счет чего образуется этот электрический ток и что является главным для того, чтобы этот ток появился.
• Прежде всего, обратимся к опыту Фарадея и посмотрим еще раз на его важные особенности.
• Итак, у нас в наличии есть амперметр, катушка с большим числом витков, которая накоротко прикреплена к этому амперметру.

Берем магнит, и точно так же, как на предыдущем уроке, опускаем этот магнит внутрь катушки. Стрелка отклоняется, то есть в данной цепи существует электрический ток.

Рис. 1. Опыт по обнаружению индукционного тока

А вот когда магнит находится внутри катушки электрического тока в цепи нет. Но стоит только попытаться этот магнит достать из катушки, как в цепи вновь появляется электрический ток, но направление этого тока изменяется на противоположное.

Обратите внимание также на то, что значение электрического тока, который протекает в цепи, зависит еще и от свойств самого магнита. Если взять другой магнит и проделать тот же эксперимент, значение тока существенно меняется, в данном случае ток становится меньше.

Проведя эксперименты, можно сделать вывод о том, что электрический ток, который возникает в замкнутом проводнике (в катушке), связан с магнитным полем постоянного магнита.

Иными словами, электрический ток зависит от какой-то характеристики магнитного поля. А мы уже ввели такую характеристику — магнитная индукция.

Напомним, что магнитная индукция обозначается буквой , это — векторная величина. И измеряется магнитная индукция в теслах.

1. [Tл] — Тесла — в честь европейского и американского ученого Николы Тесла.
2. Магнитная индукция характеризует действие магнитного поля на проводник с током, помещенный в это поле.
3. Но, когда мы говорим об электрическом токе, то должны понимать, что электрический ток, и это вы знаете из 8 класса, возникает под действием электрического поля.

Следовательно, можно сделать вывод о том, что электрический индукционный ток появляется за счет электрического поля, который в свою очередь образуется в результате действия магнитного поля. И такая взаимосвязь как раз осуществляется за счет магнитного потока.

Что же такое магнитный поток?

Магнитный поток обозначается буквой Ф и выражается в таких единицах, как вебер, и обозначается [Bб].

Магнитный поток можно сравнить с потоком жидкости, протекающей через ограниченную поверхность. Если взять трубу, и в этой трубе протекает жидкость, то, соответственно, через площадь сечения трубы будет протекать определенный поток воды.

Магнитный поток по такой аналогии характеризует, какое количество магнитных линий будет проходить через ограниченный контур. Этот контур это и есть площадка, ограниченная проволочным витком или, может быть, какой-либо другой формой, при этом обязательно эта площадь — ограниченная.

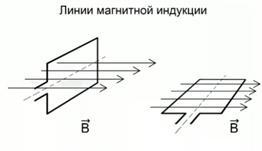
Рис. 2. В первом случае магнитный поток максимален. Во втором случае – равен нулю.

На рисунке изображены два витка. Один виток – это проволочный виток, через который проходят линии магнитной индукции. Как видите, этих линий здесь изображено четыре.

Если бы их было гораздо больше, то мы бы говорили, что магнитный поток будет большой.

Если бы этих линий было меньше, например, мы бы нарисовали одну линию, то тогда бы мы могли сказать, что магнитный поток достаточно мал, он небольшой.

И еще один случай: тогда, когда виток располагается таким образом, что через его площадь не проходят магнитные линии. Такое впечатление, что линии магнитной индукции скользят по поверхности. В этом случае можно сказать, что магнитный поток отсутствует, т.е. нет линий, которые пронизывали бы поверхность этого контура.

Магнитный поток характеризует весь магнит в целом (либо другой источник магнитного поля). Если магнитная индукция характеризует действие в какой-то одной точке, то магнитный поток – весь магнит целиком.

Можно сказать о том, что магнитный поток – это вторая очень важная характеристика магнитного поля.

Если магнитную индукцию называют силовой характеристикой магнитного поля, то магнитный поток – это энергетическая характеристика магнитного поля.

Т.о., именно под действием магнитного потока создается электрическое поле в замкнутом проводнике. А уже это электрическое поле создает не что иное, как электрический ток.

Давайте посмотрим еще раз на эксперимент, и теперь, уже зная, что существует магнитный поток, посмотрим на связь магнитного потока и значение индукционного электрического тока.

Возьмем магнит и достаточно медленно пропустим его через катушку. Значение электрического тока меняется очень незначительно.

Если же попытаться вытащить магнит быстро, то значение электрического тока будет больше, чем в первом случае.

В данном случае роль играет скорость изменения магнитного потока. Если изменение скорости магнита будет достаточно большим, значит, и индукционный ток тоже будет значительным.

В результате такого рода экспериментов были выявлены следующие закономерности.

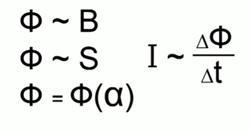
Рис. 3. От чего зависят магнитный поток и индукционный ток

1. Магнитный поток пропорционален магнитной индукции.

2. Магнитный поток прямо пропорционален площади поверхности контура, через который проходят линии магнитной индукции.

3. И третье — зависимость магнитного потока от угла расположения контура. Мы уже обращали внимание на то, что, если площадь контура тем или иным образом, это оказывает влияние на наличие и величину магнитного потока.

• Таким образом, можно сказать, что сила индукционного тока прямо пропорциональна скорости изменения магнитного потока.
• I~
• ∆Ф – это изменение магнитного потока.
• ∆t – это время, в течение которого изменяется магнитный поток.
• Отношение – это как раз и есть скорость изменения магнитного потока.
• Исходя из этой зависимости, можно сделать вывод, что, например, индукционный ток может быть создан и достаточно слабым магнитом, но при этом скорость движения этого магнита должна быть очень большой.

Первым человеком, который этот закон получил, был английский ученый М. Фарадей. Понятие магнитного потока позволяет глубже взглянуть на единую природу электрических и магнитных явлений.

Список дополнительной литературы:

Элементарный учебник физики. Под ред. Г.С. Ландсберга, Т. 2. М., 1974 Яворский Б.М., Пинский А.А., Основы физики, т.2., М. Физматлит., 2003 А так ли хорошо знакомы вам потоки?// Квант. — 2009. — № 3. — С. 32-33. Аксенович Л. А.

Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.

344.

Источник: https://interneturok.ru/lesson/physics/9-klass/elektromagnitnye-yavleniya/magnitnyy-potok-2

Электромагнитная индукция. | Объединение учителей Санкт-Петербурга

Электромагнитная индукция
1831 г. — М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, — появление, возникновение).
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи
Появление тока в замкнутом контуре при изменении магнит­ного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникно­вении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, назы­вается электромагнитной индукцией. Или: явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией.
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление):  .  e не зависит от свойств контура: . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
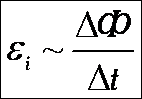
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы.
Возникновение индукционного тока — следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: ; Магнитный поток Ф­ → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: , где  — т.н. индукционное магнитное поле. В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: . Магнитный поток Ф  → ΔФ0). Ток в контуре имеет положительное направление (), если  совпа­дает с ,   (т.е. ΔΦ

Источник: https://www.eduspb.com/node/1776

Магнитный поток

Субботин Б.П.

На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.

• Определение
  магнитного потока:
• Магнитным
  потоком Ф через поверхность S называют
  количество линий вектора магнитной
  индукции B, проходящих через поверхность
  S.
• Формула
  магнитного потока:
• Ф
  = BS cos α
• здесь
  α — угол между направлением вектора
  магнитной индукции B и нормалью к
  поверхности S.

Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.

А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.

Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 108 мкс.
Соответственно 1 мкс = 10-8 вб.

Магнитный
поток является скалярной величиной.

ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА

Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции.

Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.

Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? — выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные
формулы

·            Закон
электромагнитной индукции (закон
Фарадея):

где – эдс индукции;–
полный магнитный поток (потокосцепление).

·            Магнитный
поток, создаваемый током в контуре,

где  –
индуктивность контура;–
сила тока.

·            Закон
Фарадея применительно к самоиндукции

·            Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,

где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.

·            Индуктивность
соленоида

где –
магнитная постоянная;

png» width=»19″>–
магнитная проницаемость вещества;–
число витков соленоида;

png» width=»17″>–
площадь сечения витка;–
длина соленоида.

·            Сила
тока при размыкании цепи

где –
установившаяся в цепи сила тока;

png» width=»17″>–
индуктивность контура,–
сопротивление контура;

png» width=»11″>–
время размыкания.

·            Сила
тока при замыкании цепи

·            Время
релаксации

Примеры
решения задач

Пример
1.

Магнитное
поле изменяется по закону ,
где=
15 мТл,.

 В
магнитное поле помещен круговой
проводящий виток радиусом = 20
см под угломк
направлению поля (в начальный момент
времени).

Найти эдс индукции, возникающую в
витке в момент времени=
5 с.

Решение

По
закону электромагнитной индукции возникающая в
витке эдс индукции ,
где–
 магнитный поток, сцепленный в витке.

где –
площадь витка,;

png» width=»19″>– угол
между направлением вектора магнитной
индукциии
нормалью к контуру:

png» width=»159″>.

Подставим
числовые значения: =
15 мТл,,= 20
см =   = 0,2 м,.

Пример 2В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре.РешениеПри движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции.

По
закону Фарадея ,
 где

png» width=»120″>,
тогда,
но

png» width=»58″>,
поэтому.

Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.

САМОИНДУКЦИЯ

Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.

При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.

поля и в цепи появляется
ЭДС индукции.  Это
явление называется самоиндукцией.Самоиндукция —
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.

Возникающая при этом ЭДС
называется ЭДС
самоиндукции

Проявление
явления самоиндукции

Замыкание
цепи При
замыкании в эл.

цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е.

в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.

Размыкание
цепи При
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е.

ИНДУКТИВНОСТЬ

Единицы
измерения индуктивности в
системе СИ:

Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды 
(
возможен сердечник).

ЭДС
САМОИНДУКЦИИ

ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.

Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Рм). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.

1. Магнитный
   момент единицы объема вещества
   характеризует его намагниченность
   — I,
   определяется по формуле:
2. I= Рм /V,
   (2.4)
3. где V —
   объем вещества.
4. Намагниченность
   в системе СИ измеряется, как и напряженность,
   в А/м,
   величина векторная.
5. Магнитные
   свойства веществ характеризуются объемной
   магнитной восприимчивостью — cо , величина
   безразмерная.

Если
какое-либо тело поместить в магнитное
поле с индукцией В,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В',
которое взаимодействует с намагничивающим
полем.

• В
  этом случае вектор индукции в среде (В)будет
  слагаться из векторов:
• В
  = В +
  В'(знак
  вектора опущен), (2.5)
• где В' —индукция
  собственного магнитного поля
  намагнитившегося вещества.
• Индукция
  собственного поля определяется магнитными
  свойствами вещества, которые характеризуются
  объемной магнитной восприимчивостью
  — cо,
  справедливо выражение:В' = cо В0 (2.6)
• Разделим
  на m0 выражение
  (2.6):
• В'/
  mо= cо В0 /m
• Получим: Н' = cо Н , (2.7)

но Н' определяет
намагниченность вещества I,
т.е. Н' = I,
тогда из (2.7):

I
= cоН.
(2.8)

Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН,
то внутри него индукция определяется
выражением:

В=В +
В' =
mН +mН' =
m0 (Н +
I) (2.9)

Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).

Источник: https://studfile.net/preview/5582906/page:11/

Магнетизм — Физика — Теория, тесты, формулы и задачи — Обучение Физике, Онлайн подготовка к ЦТ и ЕГЭ

Основные теоретические сведения

Сила Ампера

К оглавлению…

Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем.

Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью.

Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции.

В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл).

 Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. 

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.

Момент сил, действующих на рамку с током

Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю.

Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера.

Вращательный момент сил Ампера равен:

где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.

Сила Лоренца

К оглавлению…

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:

Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера).

Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца.

Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.

Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.

Теория о магнитном поле

К оглавлению…

Магнитное взаимодействие токов

Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером.

 Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.

 Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:

μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.

Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг.

Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом.

Даже если магнит разломать, то у каждой части будет по два разных полюса.

Вектор магнитной индукции

Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.

Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.

Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.

Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):

Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.

Магнитные свойства вещества

Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:

Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1.

У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.

Магнитный поток. Электромагнитная индукция

К оглавлению…

Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).

• Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
• Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.

При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:

1. Меняется магнитное поле.
2. Меняется площадь контура.
3. Меняется ориентация рамки относительно поля.

При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Движение проводника в магнитном поле

К оглавлению…

При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.

Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

Индуктивность. Самоиндукция. Энергия магнитного поля

К оглавлению…

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре.

Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.

Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

1. где: n — концентрация витков на единицу длины катушки:
2. ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
3. Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

• Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца

К оглавлению…

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее.

В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

Источник: https://educon.by/index.php/materials/phys/magnetizm