Определение и формулы для расчета и измерения индуктивности: в чем измеряется

В статье мы рассмотрим понятие индуктивности, что такое катушка индуктивности, подробно разберем закон Неймана или по-другому «взаимная индуктивность», покажем все на примере с формулами.

Взаимная индуктивность, формула Неймана

Предположим, что у нас есть две проводящие петли, петля номер один, взаимодействующая с ней, и петля номер два, вызывающая в ней магнитный поток, используя равенство индукции магнитного поля и определение индукции магнитного поля через векторный потенциал магнитного поля и изменив в этом потоке интеграл на поверхности, ограниченный замкнутым контуром, на интеграл по контуру, затем:

(1)

Из магнитостатики векторный магнитный потенциал магнитного поля из первой петли определяется как:

(2)

Если подставить формулу для векторного магнитного потенциала (2) в формулу для магнитного потока, ограниченного каким-либо произвольным контуром (1), то:

(3)

Очевидно, что формула (3) после перестановки круговых интегралов в одно место, эквивалентна:

(4)

Здесь R — расстояние друг от друга: dl(1) от dl(2)

Формула (4) может быть сохранена в виде разделения константы M 12 , тогда:

(5)

где

(6)

Формула для размера взаимной индукции (6) является симметричной из-за регулировки dl(1) от dl(2), то есть взаимная индукция после этого изменения не меняется, она симметрична. Очевидно, что она не зависит от времени.

 Значение M_12 в формуле (6) это формула Неймана .

 Если подставить формулу (5) в интегральную формулу Фарадея для первого цикла, аналогично и для второго цикла, то тогда закономерность взаимной индукции второй петли относительно первой петли для электродвижущей силы для двух петель выражаются в формулах:

(7)(8)

Мы видим, что закономерности для электромагнитной силы одинаковы, но они зависят от изменений длительности электрического тока во втором контуре (формула (7) ) или в первом контуре (формула (8)).

Собственная индуктивность

Здесь мы будем иметь дело только с одним контуром, который магнитно взаимодействует с самим собой.

Закон Фарадея и собственная индукция

• Мы должны иметь дело с индуктивностью, когда одна и та же цепь взаимодействует с одной и той же цепью магнетизмом, то есть это особый случай взаимной индуктивности. Мы записываем формулу для этой ситуации:
• Ф = L*I (9)
• Тогда формула для электромагнитной силы возникает после подстановки формулы (9) в закон Фарадея:

(10)

Формула для L такая же, как формула Неймана (6) , используется только двойное интегрирование по одному и тому же периметру, то есть геометрия применяется только к одной цепи.

Собственная энергия магнитной системы

Сила, создаваемая против ЭДС в индуктивности собственной цепи, зависит от электродвижущей силы, вызванной самоиндукцией, если ток течет в ней, и от того, что ее работа выполняется против электромагнитной силы ЭДС в единицу времени, равна:

(11)

Используя определение электродвижущей силы, обусловленной собственной индуктивностью (10), которая вытекает из закона индуктивности Фарадея, мы спрашиваем себя, что работа выполнялась системой, когда ток в системе с индуктивностью L от I равен нулю до некоторой ненулевой величины, поэтому мы приходим к выводу:

(12)

(13)

Это не зависит от того, как долго протекает ток, а зависит только от геометрии системы и тока, протекающего в нашей цепи, которая взаимодействует сама с собой в результате действия магнитного поля.

Катушка индуктивности

Далее мы поговорим о катушке индуктивности и способе измерения индуктивности.

Определение и теория катушек индуктивности

Катушка индуктивности — катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении, способная накапливать электромагнитную энергию в собственном магнитном поле. Обозначается – L. Внешний вид может быть различным, но если вы её мотаете самостоятельно, то будет выглядеть как-то так:

Величина индуктивности измеряется в Генри [Гн].

1 Генри – очень большая величина, поэтому применяемые в технике катушки индуктивности имеют величины: микрогенри – 10-6 (мкГн) и миллигенри – 10-3 (мГн).

Процессы, происходящие в катушке индуктивности (далее — индуктивности) на временном графике при подключении индуктивности к источнику прямоугольного однополярного сигнала, показаны на рисунке.

Из рисунка сбоку видно, реакция индуктивности на воздействие электрического тока абсолютно противоположно реакции конденсатора (ёмкости).

В момент подачи прямоугольного импульса источника тока (красный), ток индуктивности (фиолетовый) сначала равен нулю и с изменением времени увеличивается по экспоненте – индуктивность накапливает энергию, в начальный момент её внутреннее сопротивление максимально.

Напряжение на выводах индуктивности (зелёный) наоборот сначала максимально, но потом по мере накопления энергии уменьшается по экспоненте до нуля.

При пропадании входного импульса, так как индуктивность — элемент инерционный, напряжение на выводах индуктивности резко изменив полярность сначала максимально, а ток продолжает течь в том же направлении, уменьшаясь при этом по экспоненте – запасённая в индуктивности энергия иссякает.

Напряжение из отрицательной области так же по экспоненте стремится к нулю. Скорость изменения напряжения и тока зависит от значения индуктивности. Чем больше индуктивность, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Если сравнить с конденсатором — полная противоположность. Взаимосвязь тока и напряжения в индуктивности так же описывается законом Ома, с учётом реактивного сопротивления индуктивности.

Фактически, мы рассмотрели «четырёхполюсник» состоящий из катушки индуктивности и резистора, который называют интегрирующей цепочкой.

Интегрирующая цепочка чаще всего применяется для формирования пилообразных импульсов в любой радио аппаратуре и временной (ударение на «о») задержки прямоугольных импульсов.

Чтобы, Вам было понятнее, интегрирующая цепочка и получение пилообразного импульса изображены на следующем рисунке.

Для получения последнего, используется наиболее прямолинейный участок интегрированного импульса — его начало, и «обрезается» по времени или по амплитуде (порогу).

После чего, сигнал усиливается усилителем до необходимой величины.

В целях уменьшения размеров (исключения громоздкости), схемы формирования пилообразных импульсов, и схемы задержки импульсов эффективнее делать на интегрирующей цепочке состоящей из резистора и конденсатора.

Кроме функции преобразования прямоугольных импульсов, интегрирующая цепочка может применяться в качестве фильтра низких частот (ФНЧ). Индуктивность – инертный элемент.

Если к дросселю с большим значением индуктивности приложить переменное напряжение высокой частоты, в силу своей инертности, индуктивность будет не способной пропустить через себя ток, ведь индуктивности сначала надо будет запастись энергией в собственном сердечнике, а потом отдавать эту энергию.

Свойство индуктивности сопротивляться переменному электрическому току называют реактивным сопротивлением индуктивности, которое используется при конструировании частотных фильтров и колебательных контуров.

Реактивное сопротивление индуктивности обозначается XL или ZL и измеряется в Омах. Реактивное сопротивление индуктивности связано с частотой тока выражением:

Из формулы видно, что реактивное сопротивление индуктивности прямо пропорционально частоте. Другими словами, чем выше частота, тем больше реактивное сопротивление индуктивности.

Теперь представьте, что интегрирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает индуктивность. А мы из формулы теперь знаем, что индуктивность легко пропускает низкие частоты – его сопротивление минимально и плохо пропускает высокие частоты – его сопротивление максимально.

Чтобы было понятнее, изображу это на рисунке.

То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление индуктивности на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр низкой частоты на катушке индуктивности и резисторе.

Если в интегрирующей цепочке поменять местами индуктивность и резистор, то мы получим – дифференцирующую цепочку.

Все процессы в дифференцирующей цепочке происходят точно так же, как и в интегрирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для дифференцирующей цепочки.

Отличие заключается в том, что выходным элементом является не резистор, а катушка индуктивности.

Как описывалось в статье про конденсатор: если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.

Cледует добавить, частотные фильтры, выполненные на катушках индуктивности и резисторах, так же, как и на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез, имеют фильтры состоящие из конденсаторов и катушек индуктивности, но об этом в следующей статье.

Способ измерения индуктивности

Наверняка прочитав данную статью, грамотный читатель подумает: «Хм, теория это конечно хорошо, но как измерить руками значение индуктивности на практике?». Однажды этим вопросом задался и я, и собрал простую схему для проверки индуктивностей.

Источник: https://meanders.ru/induktivnost.shtml

Как измерить индуктивность мультиметром

При работе с любыми электроприборами или токопроводящими деталями, наличие измерительной аппаратуры является необходимым, будь то амперметр, вольтметр или омметр. Но для того чтобы не покупать все эти устройства, лучше обзавестись мультиметром.

Мультиметр является универсальным измерительным аппаратом, который позволяет измерить любую характеристику электричества. Мультиметры бывают аналоговые и цифровые.

Аналоговый мультиметр

Данный тип мультеметров отображает показания измерений при помощи стрелки, под которой установлено табло с различными шкалами значений. Каждая шкала отображает показания того или иного измерения, которые подписаны непосредственно на табло.

Но для новичков такой мультиметр будет не самым лучшим выбором, поскольку разобраться во всех обозначениях, которые находятся на табло довольно трудно. Это может привести к не правильному пониманию результатов измерения.

Цифровой мультиметр

В отличие от аналоговых, этот мультиметр позволяет с легкостью определять интересуемые величины, при этом его точность измерений гораздо выше по сравнению со стрелочными аппаратами.

Также наличие переключателя между различными характеристиками электричества исключает возможность перепутать то или иное значение, поскольку пользователю не нужно разбираться в градации шкалы показаний.

Результаты измерений отображаются на дисплее (в более ранних моделях – светодиодных, а в современных – жидкокристаллических). За счет этого цифровой мультиметр комфортен для профессионалов и прост и понятен в использовании для новичков.

Измеритель индуктивности для мультиметра

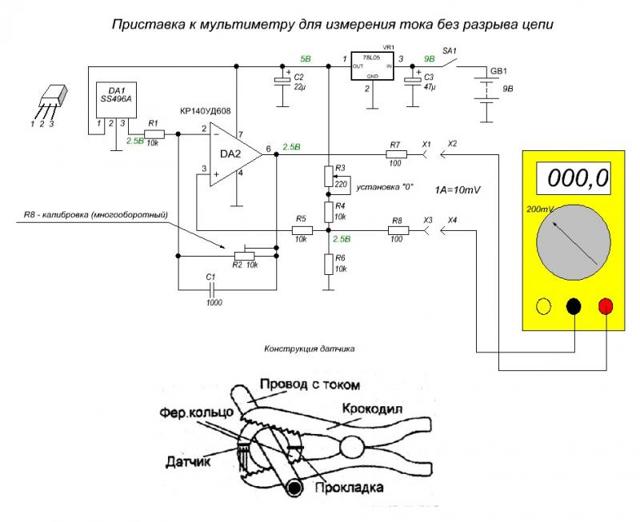
Несмотря на то, что определять индуктивность при работе с электроникой приходится редко, это все же иногда необходимо, а мультиметры с измерением индуктивности найти достаточно трудно. В данной ситуации поможет специальная приставка к мультиметру, позволяющая измерить индуктивность.

Зачастую для подобной приставки используется цифровой мультиметр установленный на измерение напряжения с порогом точности измерения в 200 мВ, который можно приобрести в любом магазине электро и радиоаппаратуры в готовом виде. Это позволит сделать простую приставку к цифровому мультиметру.

Сборка платы приставки

• 
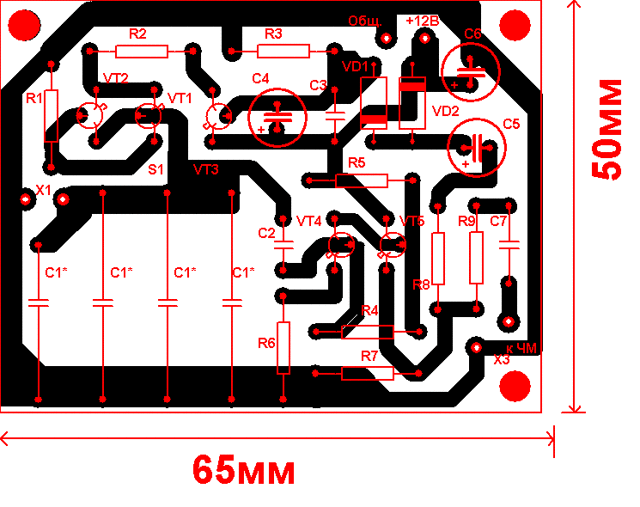
• Собрать приставку-тестер к мультиметру для измерения индуктивности можно без особых проблем в домашних условиях, обладая базовыми знаниями и навыками в области радиотехники и пайки микросхем.
• В схеме платы можно применять транзисторы КТ361Б, КТ361Г и КТ3701 с любыми буквенными маркерами, но для получения более точных измерений лучше использовать транзисторы с маркировкой КТ362Б и КТ363.

Эти транзисторы устанавливаются на плате в позициях VT1 и VT2. На позиции VT3 необходимо установить кремневый транзистор со структурой p-n-p, например, КТ209В с любой буквенной маркировкой. Позиции VT4 и VT5 предназначены для буферных усилителей.

1. Подойдет большинство высокочастотных транзисторов, с параметрами h21Э для одного не меньше 150, а для другого более 50.
2. Для позиций VD и VD2 подойдут любые высокочастотные кремневые диоды.

Резистор можно выбрать МЛТ 0,125 или аналогичный ему. Конденсатор С1 берется с номинальной емкостью 25330 пФ, поскольку он отвечает за точность измерений и ее значение стоит подбирать с отклонением не более 1%.

Такой конденсатор можно сделать объединив термостабильные конденсаторы разной емкости (например, 2 на 10000 пФ, 1 на 5100 пФ и 1 на 220 пФ). Для остальных позиций подойдут любые малогабаритные электролитические и керамические конденсаторы с допустимым разбросом в 1,5-2 раза.

Контактные провода к плате (позиция Х1) можно припаять или подключать при помощи пружинящих зажимов для «акустических» проводов. Разъем Х3 предназначен для подключения приставки к мультиметру (частотомеру).

При необходимости регулирования диапазона измерений на плату можно добавить разъем для переключателя (например, на три диапазона).

Корпус приставки к мультиметру

Корпус можно сделать из уже готового короба подходящего размера или сделать короб самостоятельно. Материал можно выбрать любой, например, пластик или тонкий стеклотекстолит. Короб делается под размер платы, и в нем подготавливаются отверстия для ее крепления. Также делаются отверстия для подключения проводки. Все фиксируется небольшими шурупами.

Питание приставки осуществляется от сети при помощи блока питания с напряжением в 12 В.

Настройка измерителя индуктивности

Для того чтобы откалибровать приставку для измерения индуктивности понадобятся несколько индукционных катушек с известной индуктивность (например, 100 мкГн и 15 мкГн).

Катушки по очереди подключаются к приставке и, в зависимости от индуктивности, движком подстроечного резистора на экране мультиметра выставляется значение 100,0 для катушки на 100 мкГн и 15 для катушки на 15 мкГн с точностью 5%.

По такому же методу устройство настраивается и в других диапазонах. Важным фактором является то, что для точной калибровки приставки необходимы точные значение тестовых катушек индуктивности.

Альтернативным методом определения индуктивности является программа LIMP. Но этот способ требует некоторой подготовки и понимания работы программы.

Но как в первом, так и во втором случае точность подобных измерений индуктивности будет не очень высока. Для работы с высокоточным оборудованием данный измеритель индуктивности подходит плохо, а для домашних нужд или для радиолюбителей будет отличным помощником.

Проведение замеров индуктивности

После сборки приставку к мультиметру необходимо протестировать. Есть несколько способов, как проверить устройство:

1. Определение индуктивности измерительной приставки. Для этого необходимо замкнуть два провода, предназначенных для подключения к индуктивной катушке. Например, при длине каждого провода и перемычки 3 см образуется один виток индукционной катушки. Этот виток обладает индуктивностью 0,1 – 0,2 мкГн. При определении индуктивности свыше 5 мкГн данная погрешность не учитывается в расчетах. В диапазоне 0,5 – 5 мкГн при измерении необходимо брать в расчет индуктивность устройства. Показания менее 0,5 мкГн являются примерными.
2. Измерение неизвестной величины индуктивности. Зная частоту катушки, при помощи упрощенной формулы расчета индуктивности можно определить это значение.
3. В случае, когда порог срабатывания кремниевых p-n переходов выше амплитуды измеряемой электрической цепи (от 70 до 80 мВ), можно измерить индуктивность катушек непосредственно в самой схеме (предварительно обесточив ее). Поскольку собственная емкость приставки имеет большое значение (25330 пФ), погрешность подобных измерений будет составлять не более 5% при условии, что емкость измеряемой цепи не превышает 1200 пФ.

При подключении приставки непосредственно к катушкам расположенным на плате применяется проводка длиной 30 сантиметров с зажимами для фиксации или щупами. Провода скручиваются с расчетом один виток на сантиметр длины. В таком случае образуется индуктивность приставки в диапазоне 0,5 – 0,6 мкГн, которую также необходимо учитывать при измерениях индуктивности.

Источник: https://EvoSnab.ru/instrument/avo/izmerenie-induktivnosti-multimetrom

Что такое активная и реактивная мощность переменного электрического тока?

Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.

Мощность в цепи переменного электрического тока

Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.

Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.

В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания.

Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.

При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.

Понятие активной мощности

Активная “полезная” мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).

  Как проверить конденсатор на работоспособность мультиметром?

Рассчитывается по формуле: P = U⋅I⋅cosφ,

где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.

ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73

Понятие реактивной мощности

Реактивная “вредная” мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.

Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.

Обозначается эта величина латинской буквой Q.

ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).

• Рассчитывается по формуле:
• Q = U⋅I⋅sinφ,
• где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.

ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.

Емкостные и индуктивные нагрузки

Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.

Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.

ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.

Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.

ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.

Коэффициент мощности cosφ

Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.

Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.

ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.

Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.

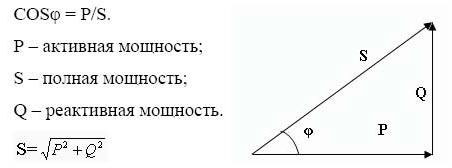
Понятие полной мощности. Треугольник мощностей

Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.

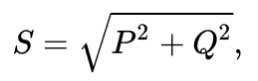
Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.

S = U⋅I

ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).

Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.

Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.

Как найти активную, реактивную и полную мощности. Пример расчета

Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.

Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.

Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.

Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.

Как измеряют cosφ на практике

Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.

Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.

1. Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
2. Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.

Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.

Источник: https://odinelectric.ru/knowledgebase/aktivnaja-i-reaktivnaja-moshhnost-peremennogo-toka

Индуктивность (коэффициент самоиндукции)

1). Индуктивность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

В формуле

Ф  — магнитный поток,  I  — ток в контуре,  L  — индуктивность.

Нередко говорят об индуктивности прямого длинного провода. В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведённое выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током:

Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников.

Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются и устройства, не основанные на электромагнитной индукции (см.

 Гиратор); такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью (хотя вообще говоря с определёнными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.

Обозначение и единицы измерения:

В системе единиц СИ индуктивность измеряется в генри, сокращённо Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.

В вариантах системы СГС — системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн); для сантиметров в качестве единиц индуктивности применяется также название абгенри.

В системе СГСЭ единицу измерения индуктивности либо оставляют безымянной, либо иногда называют статгенри (1 статгенри ≈ 8,987552·1011 генри, коэффициент перевода численно равен 10-9 от квадрата скорости света, выраженной в см/с).

Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

Материал из Википедии — свободной энциклопедии

2). Индуктивность, коэффициент самоиндукции (L) — отношение потокосцепления самоиндукции цепи к силе тока в ней.

Индуктивность кольцевой катушки L=μaW2S/l, где W — количество витков; S — поперечное сечение катушки; l — длина катушки; μa — магнитная проницаемость среды.

Словарь по электротехнике

Источник: https://elektro911.ru/dir/russkij_alfavit/i/induktivnost_koehfficient_samoindukcii/11-1-0-114

Индуктивность — это… Что такое Индуктивность?

Индуктивность микрополосковой линии является распределенной и характеризуется значением индуктивности на единицу длины.

Катушка индуктивности.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].

В формуле

 — магнитный поток,  — ток в контуре,  — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:

.

Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].

Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см.

Гиратор); такому элементу можно приписать определенную эффективную индуктивность, используемую в расчетах полностью (хотя вообще говоря с определенными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.

В вариантах системы СГС — системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн)[4]; для сантиметров в качестве единиц индуктивности применяется также название абгенри.

Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz)[8][9]. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)[10]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года[11].

Теоретическое обоснование

• Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[4].
• Будем здесь вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля не настолько сильны и быстры, чтобы ими нельзя было пренебречь в смысле порождения ими магнитного поля.
• Ток считаем одинаковым по всей длине контура (пренебрегая емкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства пропорциональна этому току.

Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником также пропорционально порождающему току.

Рассуждение выше верно для вакуума.

В случае присутствия магнитной среды[12] (магнетика) с заметной (или даже большой) магнитной восприимчивостью вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме).

Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остается пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной.

На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближенно рассчитать поток через нее (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже).

Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).

Итак, мы обосновали:

~

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур.

(Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть ее краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй).

Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмем две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.

Свойства индуктивности

• Индуктивность[13] всегда положительна.
• Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника).[14]

Индуктивность одновиткового контура и индуктивность катушки

Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом[4]:

где  — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду:

где  — сумма магнитных потоков через все витки (это так называемый полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока вообще в случае для катушки в общем определении индуктивности и в теоретическом рассмотрении выше; однако для упрощения и удобства для многовитковых катушек в электротехнике пользуются отдельным понятием и отдельным обозначением), а  — уже индуктивность многовитковой катушки. называют потокосцеплением или полным магнитным потоком[15]. Коэффициент пропорциональности иначе называется коэффициентом самоиндукции контура или просто индуктивностью[4].

Если поток, пронизывающий каждый из витков одинаков (что довольно часто можно считать верным для катушки в более или менее хорошем приближении), то .

Соответственно, (суммарный магнитный поток через каждый виток увеличивается в N раз — поскольку его создают теперь N единичных витков, и потокосцепление еще в N раз, так как это поток через N единичных витков).

Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки).

При этих условиях и без использования магнитного материала плотность магнитного потока внутри катушки является фактически постоянной и (приближенно) равна

где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим[16], что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :

Отсюда следует формула для индуктивности соленоида (без сердечника):

В случае, когда , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника слишком во много раз.

Более точные формулы для соленоида конечного размера

1. Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[18]:
2. где

— количество витков,
— радиус цилиндра,
— длина его образующей,
,
,
— Эллиптические интегралы.

Это дает

• для

• для

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Тороидальная катушка

Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближенно пользоваться формулой для бесконечного прямого соленоида (см. выше):

где — оценка длины соленоида ( — большой радиус тора).

Лучшее приближение дает формула

где предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.

Индуктивность длинного прямого проводника

Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближенной формулой[19]:

где − магнитная постоянная, — относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума ), — относительная магнитная проницаемость материала проводника, — длина провода, — радиус его сечения.

Индуктивность единичного круглого витка

Индуктивность витка в форме окружности[19] радиуса R из проводника круглого сечения радиусом r

Источник: https://biograf.academic.ru/dic.nsf/ruwiki/1583971/biograf.academic.ru/dic.nsf/ruwiki/100815

Измерение электрического сопротивления, емкости, индуктивности с помощью обычного ПK

КомпьютерыОригинальная идея программиста, нестандартный подход к стандартному оборудованию ПК и совсем незначительные ухищрения с аппаратной частью позволяют превратить обычный компьютер в цифровой мультиметр.

Радиолюбители знают, как важно иметь под рукой средство для измерения емкости конденсаторов и индуктивности дросселей, меньше проблем возникает при измерении сопротивления резисторов. Это нужно при как при подстройке электронных схем, так и для проверки деталей.

К тому же у производителей уже давно вошло в моду не ставить маркировку на корпусах множества радиодеталей. Со временем скапливается огромное количество не промаркированных конденсаторов и дросселей с неизвестной индуктивностью. На вид они могут быть абсолютно одинаковые, а номиналы отличаются в тысячи раз.

Определить это можно только измерением параметров. При этом обычно не требуется какая-то исключительная точность, достаточно той, с которой маркируется большинство радиодеталей, чаще всего 10%. В былые времена таких приборов хоть сколь приличного качества в продаже не было. Теперь появилась масса импортной измерительной техники.

Но что-то мне не попадались мультиметры способные измерять емкость и индуктивность стоимость которых была бы по карману. Однако оказалось, что эту проблему можно решить совершенно неожиданным путем – с помощью оригинальной идеи переложить все бремя измерений на компьютер, даже ничего не меняя в его конструкции.

Тем, что компьютер может стать главным звеном в измерительной или аналитической аппаратуре уже никого не удивишь. Обычно для этих целей используются специальные модули или платы расширения – редкое и дорогостоящее оборудование.

Совсем другое дело превратить в цифровой мультиметр самый обычный компьютер, в его стандартной конфигурации, без каких либо дополнительных аппаратных доработок и финансовых затрат.

Оригинальная идея программиста, нестандартный подход к стандартному оборудованию ПК и совсем незначительные ухищрения с аппаратной частью позволяют воплотить эту возможность в жизнь. Измерительный прибор из ПК получается с помощью одних только программных средств.

Но для начала стоит разобраться с физикой данного вопроса, возможно после экскурса к слегка призабытым знаниям, подобная реализация ПК уже не будет казаться чем-то фантастическим.

Существует два вида электрического сопротивления: активное и реактивное. Активное сопротивление (R) – это обычные резистор, сопротивление которого, в общем-то, не зависит от рода тока.

Реактивное сопротивление – это сопротивление катушек индуктивности (дросселей) и конденсаторов. Величина реактивного сопротивления уже зависит от частоты тока.

Так на постоянном токе реактивное сопротивление конденсатора устремляется к бесконечности, а дросселя наоборот – к нулю (без учета активной составляющей сопротивления провода).1

Xc = 1/2pfC 2где Xc – сопротивление, Ом; f – частота, Гц; С – емкость, Ф.

Электрическое сопротивление конденсатора переменному току можно измерить. Зная сопротивление и частоту тока, легко по формуле вычислить емкость. Кроме того, если в электрической цепи стоит конденсатор происходит сдвиг фаз напряжения и тока. Причем ток опережает напряжение на величину 90°.

Реактивное сопротивление катушки индуктивности с увеличением частоты возрастает:

XL = 2pfL где XL – сопротивление катушки, Ом; f – частота, Гц; L – индуктивность, Гн.

Индуктивность дросселя легко вычисляется по известному сопротивлению и заданной частоте тока. При этом фазы напряжения и тока на катушке индуктивности сдвигаются относительно друг друга, и теперь ток отстает от напряжения на 90°.

Для измерения реактивного сопротивления емкости и индуктивности потребуется, прежде всего, переменный ток синусоидальной формы. С задачей программного генератора с легкостью может справиться звуковая плата компьютера.

Другая проблема – определение величины электрического сопротивления измеряемого элемента.

Но оказывается и эту задачу можно решить программным путем, с помощью той же звуковой платы, не прибегая к специальным аналого-цифровым преобразователям.

Все это делает программа Multi Meter, используя весьма оригинальный способ для измерения электрического сопротивления, емкости и индуктивности. Работает под управлением Windows9X в минимальной конфигурации CPU 486DX4, 16M RAM. Программа бесплатна и найти ее и описание к ней можно по адресу www.i-adrian.home.ro.

В качестве измерительного преобразователя Multi Meter используется обычная звуковая карта. Принцип действия прост. Так как звуковая карта не является полноценным АЦП, – хорошо чувствуя форму сигнала, она совершенно не приспособлена для определения его амплитуды, прямым путем, конечно.

Но оказалось, что это ограничение можно обойти, используя сравнение уровней двух независимых сигналов. Генерируемый сигнал переменного тока с выхода Line-Out поступает на линейный вход Line-In. По одной цепи сигнал с Line-Out идет напрямую, без всякого сопротивления на левый линейный вход звуковой карты – это эталонный сигнал.

Так же вводится дополнительный резистор (R serial), который устанавливается снаружи корпуса системного блока и соединяется одним концом на корпус. Понятно, что уровень сигнала с правого входа Line-In, прошедшего через сопротивление, будет меньше, чем с левого.

Программа измеряет соотношение уровней сигналов с левого и правого входов, и по нему вычисляется активное сопротивление для обычного резистора. Для реактивной нагрузки емкости и индуктивности алгоритм несколько усложняется, используется две частоты, кроме ослабления сигнала так же учитывается сдвиг фаз.

Емкость конденсаторов и индуктивность дросселей определяется путем решения системы из двух уравнений. Для подсоединения к разъемам звуковой карты понадобится два штекера, разводка которых показана на (рис.2).

Multi Meter состоит из одного исполнимого файла (212кб) и не требует инсталляции, ее интерфейс прост и понятен (рис.3). Слева в области «Work mode» задаются режимы калибровок и измерений. Сначала программа калибруется. В режиме «short» запускается с замкнутой накоротко измерительной цепью (точки А и Б), без всякого сопротивления.

При этом нужно подождать некоторое время, пока в окне «Err» не установиться наименьшее числовое значение. Таким же способом калибровка проделывается в режиме «open», но уже при разомкнутой измерительной цепи. Режим «Measure 1st mtd» используется для измерения сопротивления резисторов.

В положении «Measure 2nd mtd» измеряется емкость или индуктивность.

В левых верхних окнах пользователем задаются значения генерируемых для измерения частот и сопротивление установленного дополнительного резистора R serial. Эти параметры могут быть разными для различных режимов и величин измерений, что будет уточнено ниже.

Однако действительным будет только то значение, которое соответствует роду измеряемой величины.

Значения частот Multi Meter могут лежать в интервале 50…1000 Гц. При измерении сопротивления обычного резистора подбор частоты не так важен. Обе частоты применяются в режиме «Measure 2nd mtd», при этом разница между ними (левом/правом окне), согласно рекомендациям разработчика, не должна быть меньше 10% и больше 200%.

Хотя последнее условие и не является обязательным. Сопротивление резистора R serial может находиться в пределах 20…1000 Ом (чаще 20…100 Ом), в зависимости от режима и диапазона измерений. Величина сопротивления R serial должна указываться в окне программы с большой точностью.

Как показывает практика, при погрешности указанного значения от действительного сопротивления более чем на 1% резко возрастет конечная погрешность измерений Multi Meter.

Надо учитывать, что маркировка резисторов обычно наносится с погрешностью 5; 10%, поэтому реальные сопротивления для набора резисторов R serial нужно определить с помощью другого точного прибора или использовать высокоточные детали.

Автор программы дает следующие рекомендации по подбору сопротивления R serial и частот сигнала (Yamaha 724) для Multi Meter v.0.03:

  • При измерении емкости конденсаторов номиналом 0,22мкф и выше рекомендуется R serial 20 Ом и частоты 100/1000 Гц. Для измерения конденсаторов меньших номиналов рекомендуется увеличивать частоты и сопротивление R serial, но не более чем 1000 Ом.

  • Для измерения резисторов номиналом от 1 Ом до 10 кОм рекомендуется R serial 20 Ом, частоты не оговариваются. Насчет измерения индуктивности никаких рекомендаций нет.

  • Уровень сигнала на линейном входе и выходе в микшере Windows рекомендуется поставить на середину, но не выше 3/4. Хотя может оказаться, что эти уровни нуждаются в более скрупулезной настройке.

Я со своей стороны провел всесторонние практические испытания Multi Meter 0.03, перемерив огромное количество радиоэлементов. На основе собственного опыта были определены оптимальные значения R serial и наборы частот для тех или иных режимов и диапазонов.

Так же на практике были установлены возможности Multi Meter в связке с саундкартой Yamaha 724 производства Genius. Определялись диапазоны значений, в которых программа еще могла нормально работать, а так же погрешности измерений.

Начнем с резисторов. Измерения проводились в режиме «Measure 1st mtd». Частоты 300/500, хотя в данном случае их значения не имеют большого значения. Измерение резисторов проводились при различных сопротивлениях R serial: 20…500 Ом. При установке R serial 20 Ом оптимальный интервал для измерения сопротивлений соответствовал 1…20000 Ом.

В этом диапазоне максимальная погрешность была не хуже 5%. Данные сверялись с показаниями аппаратного цифрового мультиметра. Этот результат можно считать хорошим, учитывая, что резисторы для ширпотреба маркируются с 5% и 10% точностью. Увеличить верхний предел измерений удается увеличением R serial.

При значении R serial 100 Ом верхний предел можно поднять уже до 150 кОм. Еще выше поднять верхний предел – до 500 кОм удается с помощью R serial 300 Ом. Хотя в последнем случае уже начинает расти погрешность низкоомных резисторов, этот режим рекомендуется применять для резисторов номиналом не ниже 200 Ом.

Дальнейшее увеличение сопротивления R serial уже ник чему не приводило.

Емкость конденсаторов с помощью Multi Meter удавалось измерять в диапазоне от 1 нф до 1000 мкф независимо от типа. Режим программы – «Measure 2nd mtd». Для диапазона от 10 нф и выше рекомендуется использовать R serial 20 Ом и частоты 100/1000.

К сожалению я не располагал каким либо другим точным прибором для измерения емкости, по которому можно было бы сверять результаты для определения погрешности измерений Multi Meter’ом. По моему субъективному заключению погрешность измерения емкости в этом режиме не хуже 5…6%.

Для конденсаторов меньшей емкости лучше использовать R serial 100 Ом и частоты 500/1000: погрешность здесь в интервале 1…10 нф – около 10%; а от 10 нф до 200 мкф – те же 5…6%; для более высоких номиналов этот режим не рекомендуется.

Таким образом Multi Meter охватывает большую часть диапазона наиболее часто используемых конденсаторов, причем, с хорошей точностью измерений, учитывая, что обычные конденсаторы маркируются с 10% и 20% точностью, а электролиты чаще с 20%.

Индуктивность дросселей мне удавалось довольно точно измерять в диапазоне от 4 мкГн до 120мГн (выше просто не было чего измерять). Опять же не было точного прибора, с помощью которого можно было бы сравнивать показания.

Для тех трех десятков дросселей, что были у меня, я думаю, максимальная погрешность была не хуже 5%. При этом был установлен R serial 20 Ом и частоты 700/1000. При индуктивности ниже 4 мкГн Multi Meter давал сначала заниженные показания, а потом и вовсе нули.

Нижний предел можно еще попробовать опустить где-то до 2 мкГн, установив частоты 900/1000, однако здесь падает общая стабильность.

Недостатком Multi Meter является зависимость результатов измерений от уровней Line-Out, Line-In сигнала. Сказываются слишком завышенные или заниженные уровни. Надо учитывать, что у разных звуковых карт уровни могут существенно отличаться. Предусмотренная в программе калибровка по короткозамкнутой и разомкнутой измерительной цепи в этом случае ничего не дает.

Поэтому калибровать Multi Meter приходится вручную, выставляя в микшере уровни Line-Out, Line-In, сверяясь по известным номиналам измеряемых элементов. В моем случае, практика показала, что, выставив уровни сигнала входа/выхода по резисторам, программа давала действительные результаты и в случае емкостей и индуктивности.

Все полученные результаты относятся к системе со звуковой картой на чипе Yamaha 724 производства Genius, под Windows 98SE на довольно мощной машине. Я не могу обещать, что на других платах, ввиду индивидуальных особенностей их схемных решений, результаты в точности повторятся.

Наверное, придется поэкспериментировать и подобрать другие параметры уровней Line-Out, Line-In, возможно, частот и сопротивлений R serial.

Нужно только знать в каких граничных диапазонах измерений реально может работать та или иная звуковая карта. Конечно, точность Multi Meter не прецизионная, но достаточно хорошая – это, еще смотря, с чем сравнивать. Если для сопротивления резисторов можно купить достаточно точный цифровой прибор (порядка 10$), то с емкостью и индуктивностью не так все просто.

Такие приборы либо очень дороги, либо дают диапазон и погрешность еще хуже программы Multi Meter и тоже стоят денег. Так обстоят дела с дешевыми стрелочными тестерами, у которых имеются шкалы для L и C. Кроме того, последние берут сигнал переменного тока с розетки 220 В, что небезопасно для человека и самого прибора. Я остался очень доволен тем результатом, который был получен.

Стоит отдать должное автору Multi Meter за оригинальность подхода.

От редакции Мы рекомендуем использовать для подобных измерений не линейный выход звуковой карты (он обычно имеет достаточно высокое выходное сопротивление, что плохо скажется на точности измерений с эталонным резистором Rserial меньше 100 Ом), а выход звуковой карты на наушники (его выходное сопротивление меньше 1 Ома, что достаточно для подобных измерений). В дешевых звуковых картах линейный выход иногда уже является и выходом на наушники (имеется встроенный усилитель). Видимо, так и обстояло дело в указзанной автором статьи карте Genius. При измерениях небольших индуктивностей и емкостей рекомендуем использовать как можно более короткие внешние провода (в идеале — подлючать элементы прямо к миниджеку, воткнутому в линейный вход карты.)

1. Имеется ввиду синусоидальный (гармонический) сигнал переменного тока. вернуться

2. p — число «пи»=3,1415926. вернуться

Источник: https://www.ferra.ru/review/computers/s21347.htm