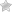Определение механического резонанса: амплитуда, период, частота колебаний.

• В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
• Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
• Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
• Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
• Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
• В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.
• Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
• Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:

Эти уравнения называют кинематическим законом гармонического движения.

Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.

Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.

Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.

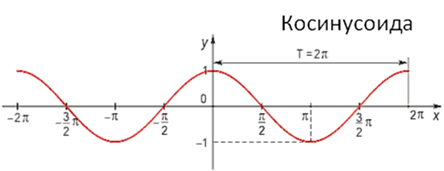
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа

Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.

Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.

Теперь разберемся с величинами, входящими в уравнение колебательного движения.

1. Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
2. Амплитуда колебаний — максимальное смещение тела от положения равновесия.
3. Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
4. j0 — это начальная фаза колебаний.
5. Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
6. Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
7. Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.

Число колебаний в единицу времени называется частотой колебаний.  Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.

• Период колебания и частота колебаний связаны следующей зависимостью:

Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.

1. Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
2. Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
3. При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.

Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона.

Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.

Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.

Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.

Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.

• Основные выводы:
• – Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
• – Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
• – Амплитуда колебаний — максимальное смещение тела от положения равновесия.
• – Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
• – Число колебаний в единицу времени называется частотой колебаний.
• – Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
• – Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
• – Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
• – Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.

Источник: https://videouroki.net/video/27-garmonichieskiie-koliebaniia-amplituda-pieriod-i-chastota-koliebatiel-nogho-dvizhieniia.html

Механические колебания и волны – FIZI4KA

ЕГЭ 2018 по физике ›

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Отличительными признаками колебательного движения являются:

• повторяемость движения;
• возвратность движения.

Для существования механических колебаний необходимо:

• наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
• наличие малого трения в системе.

Механические волны – это процесс распространения колебаний в упругой среде.

Виды волн

• Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин. Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.

• Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения. Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.

Важно! Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

где ​( x )​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​( A )​ – амплитуда колебаний; ​( omega t+varphi_0 )​ – фаза колебаний; ​( omega )​ – циклическая частота; ​( varphi_0 )​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний Скорость гармонических колебаний есть первая производная координаты по времени:

где ​( v )​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний Ускорение гармонических колебаний есть первая производная скорости по времени:

где ​( a )​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ​( F )​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

• Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
• Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где ​( W_k )​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

1. Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
2. При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно. В положении равновесия:

• потенциальная энергия равна нулю;
• кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

• кинетическая энергия равна нулю;
• потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно! Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Амплитуда и фаза колебаний

Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия. Обозначение – ​( A, (X_{max}) )​, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени. Обозначение – ​( varphi )​, единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний. Фаза гармонических колебаний в процессе колебаний изменяется.

​( varphi_0 )​ – начальная фаза колебаний.

Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно! Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период колебаний

Период колебаний – это время одного полного колебания. Обозначение – ​( T )​, единицы измерения – с.

Период гармонических колебаний – постоянная величина.

Частота колебаний

Частота колебаний – это число полных колебаний в единицу времени. Обозначение – ​(
u )​, единицы времени – с-1 или Гц (Герц).

• 1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
• Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд. Обозначение – ​( omega )​, единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

• при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
• силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.

При наличии сил трения свободные колебания будут затухающими. Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

1. Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
2. Период колебаний математического маятника:
3. Частота колебаний математического маятника:
4. Циклическая частота колебаний математического маятника:
5. Максимальное значение скорости колебаний математического маятника:
6. Максимальное значение ускорения колебаний математического маятника:
7. Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
8. Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
9. Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
10. Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ​( h )​, определяется по формуле:
11. где ​( l )​ – длина нити, ​( alpha )​ – угол отклонения от вертикали.
12. Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
13. Период колебаний пружинного маятника:
14. Частота колебаний пружинного маятника:
15. Циклическая частота колебаний пружинного маятника:
16. Максимальное значение скорости колебаний пружинного маятника:
17. Максимальное значение ускорения колебаний пружинного маятника:
18. Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
19. Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

Важно! Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.

Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.

Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.

Резонанс

• Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
• Условие резонанса:
• ​( v_0 )​ – собственная частота колебаний маятника.

На рисунке изображены резонансные кривые для сред с разным трением.

Чем меньше трение, тем выше и острее резонансная кривая.

Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях. Также резонанс используется в акустике, радиотехнике и т. д.

Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах. Обозначение – ​( lambda )​, единицы измерения – м.

1. Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
2. Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​(
  u )​ < 16 Гц);
• звуковой диапазон (16 Гц < ( u ) < 20 000 Гц);
• ультразвук ((
  u ) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

• от упругих свойств среды:

• в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
• в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.
• Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны. Шум – хаотическая смесь тонов.

Основные формулы по теме «Механические колебания и волны»

Источник: https://fizi4ka.ru/egje-2018-po-fizike/mehanicheskie-kolebanija-i-volny-2.html

Амплитуда колебаний — определение, характеристика и формулы

Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах. 

Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.

Амплитуда колебаний

Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах. 

За амплитудой можно наблюдать на простом примере пружинного маятника.

 

• В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:
• x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
• где 

• величина А – это амплитуда свободных движений груза на пружине;
• (ωt + φ0) – это фаза свободных колебаний, где ω — это циклическая частота, а φ0 – это начальная фаза, когда t = 0. 

В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой. 

Период колебаний

1. Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.

    

2. В физике период обозначают буквой Т и описывают формулами:

Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.

Частота колебаний

Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F. 

• Данная величина описывается выражением:
• v = n/t – количество колебаний за промежуток времени,
• где 

• n – это единица колебаний;
• t – отрезок времени.

В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса. 

Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -1035 Гц при одинаковой скорости.

Циклическая частота

В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой. 

1. Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
2. ω = 2π/T = 2πν.

Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике. 

• Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
• WLC = 1/LC.
• Тогда как обычная циклическая резонансная частота выражается:
• VLC = 1/2π*√ LC.

В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.

Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса. 

К ним относят:

• расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
• наибольшее отклонение – амплитуда смещения А;
• фаза колебания – определяет состояние колебательной системы в любой момент времени;
• начальная фаза колебательного процесса – когда t = 0, то φ = φ0.

Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.

Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.

Источник: https://nauka.club/fizika/amplituda-kolebaniy.html

I. Механика

Особый вид неравномерного движения — колебательное. Это движение, которое повторяется с течением времени. Механические колебания — это движения, которые повторяются через определенные промежутки времени. Если промежутки времени одинаковые, то такие колебания называются периодическими.

Колебательная система

Это система взаимодействующих тел (минимум два тела), которые способны совершать колебания. Простейшими колебательными системами являются маятники.

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

Циклическая частота характеризует скорость изменения фазы колебаний.

• Начальное состояние колебательной системы характеризует начальная фаза
• Амплитуда колебаний A — это наибольшее смещение из положения равновесия
• Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.
• Частота колебаний — это число полных колебаний в единицу времени t.

Частота, циклическая частота и период колебаний соотносятся как

Виды колебаний

Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).

Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).

При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.

Вынужденные колебания. Резонанс

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Вынужденные колебания

Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.

Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.

Примеры резонанса

Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать

Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.

Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.

В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.

Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден.

Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах.

Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.

Источник: https://fizmat.by/kursy/kolebanija_volny/kolebatelnoe

2.5. Вынужденные колебания. Резонанс. Автоколебания



Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.

Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

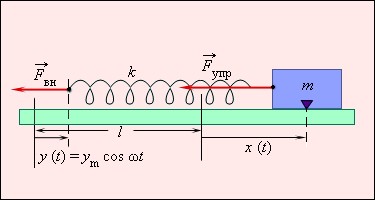
Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону где ym – амплитуда колебаний, ω – круговая частота.

Рисунок 2.5.1.Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно:

Δl = x – y = x – ym cos ωt.

Второй закон Ньютона для тела массой m принимает вид :

ma = –k(x – y) = –kx + kym cos ωt.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: Тогда уравнение вынужденных колебаний запишется в виде

(**)

где – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:

Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний (*) (см. §2.2) уравнение вынужденных колебаний (**) содержит две частоты – частоту ω0 свободных колебаний и частоту ω вынуждающей силы.

Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону

Амплитуда вынужденных колебаний xm и начальная фаза θ зависят от соотношения частот ω0 и ω и от амплитуды m>ym внешней силы.

На очень низких частотах, когда ω 

Источник: https://physics.ru/courses/op25part1/content/chapter2/section/paragraph5/theory.html

Механические колебания

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Гармонические колебания

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

• Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
• (1)
• Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

1. (2)
2. (3)
3. Измеряется циклическая частота в рад/с (радиан в секунду).
4. В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
5. .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

Уравнение гармонических колебаний

• Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
• . (4)
• Теперь дифференцируем полученное равенство (4):
• . (5)
• Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
• . (6)
• Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
• . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением.

Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Пружинный маятник

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

1. Тогда соотношение (8) принимает вид:
2. или
3. .
4. Мы получили уравнение гармонических колебаний вида (6), в котором
5. .
6. Циклическая частота колебаний пружинного маятника, таким образом, равна:
7. . (9)
8. Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
9. . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

Математический маятник

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

• Запишем для маятника второй закон Ньютона:
• ,
• и спроектируем его на ось :
• .

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

1. .
2. Итак, при любом положении маятника имеем:
3. . (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

• ,
• или
• .
• Это — уравнение гармонических колебаний вида (6), в котором
• .
• Следовательно, циклическая частота колебаний математического маятника равна:
• . (12)
• Отсюда период колебаний математического маятника:
• . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

1. Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
2. Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
3. .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний.

Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими.

Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний.

Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе.

При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Источник: https://ege-study.ru/ru/ege/materialy/fizika/mexanicheskie-kolebaniya/