g84jsm9tB4S
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением.
Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником.
Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.
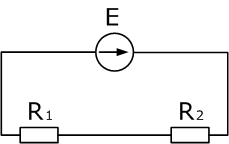
Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
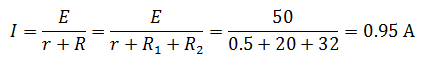
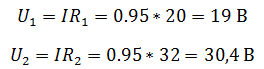
Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
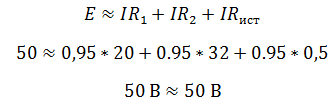
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
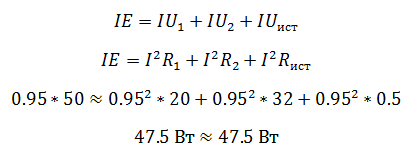
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
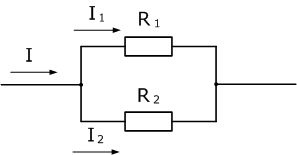
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
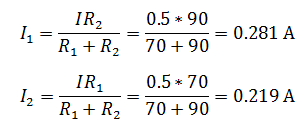
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
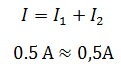
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
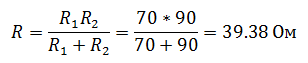
- А затем напряжение
- Зная напряжения, найдем токи, протекающие через резисторы
- Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом.
Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Интернет магазин паровой утюг
- Эквивалентное сопротивление и ток в цепи
- Отсюда мощность, выделяемая на R 1
- Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
- Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
- Таким образом производится расчет простых цепей постоянного тока.
- Резистор тока выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи, создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.
Помимо номинального сопротивления, одним из наиболее важных параметров резистора является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность – это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.
Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А),
Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт – 0,5 Ватт в данном случае – минимум.
Мощность резистора может зависеть от его размеров. Как правило, чем меньше резистор — тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:
Рассмотрим на примере: номинальное сопротивление нашего резистора тока – 100 Ом. Через него течет ток 0,1 Ампер. Чтобы узнать мощность, на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),
- P(Вт) – мощность,
- R(Ом) – сопротивление цепи (в данном случае резистора),
- I(А) – ток, протекающий через резистор.
Внимание! При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А . Это же касается и других величин.
Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)
Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор с мощностью в 1,5 – 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.
Бывает, что ток, протекающий через резистор неизвестен. Для расчёта мощности в таком случае предусмотрена специальная формула:
Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.
Например, нам необходимо произвести замену резистора тока сопротивлением 100 Ом. Ток, протекающий через него – 0,1 Ампер. Соответственно, его мощность – 1 Ватт.
Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом – 0,2 Вт, мощность резистора на 80 Ом – 0,8 Вт.
Стандартный ряд мощностей поможет выбрать резисторы тока:
Как починить москитную сетку ручки
R1 – 20 Ом (0.5 Вт)
R2 – 80 Ом (1 Вт)
Из всего вышесказанного можно сделать вывод, что разное сопротивление резисторов гарантирует их разную выделяемую мощность, так как она распределяется между резисторами разных номиналов.
Если не учитывать это обстоятельство, то можно столкнуться с большим количеством трудностей. Если один из резисторов выбран неправильно – второй работает в тяжелом температурном режиме.
Также присутствует угроза возгорания резистора из-за несоблюдения правил мощности.
Для того, чтобы сэкономить время и не рассчитывать мощность каждого отдельного резистора тока нужно запомнить одно простое правило: мощность заменяемого резистора должна быть равна мощности каждого резистора, составляющего параллельную или последовательную цепь. То есть при замене резистора мощностью 0,5 Вт надо следить за тем, чтобы каждый из резисторов для замены имел мощность не менее 0,5 Вт.
При параллельном соединение резисторов важно помнить, что чем меньше сопротивление резистора, тем больший ток через него протекает, а значит на нем будет рассеяна большая мощность.
В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.
Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.
Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
- I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
- В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
- Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.
Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
Как починить сломанную ножку стула
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).
Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А.
Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств.
Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
Параллельное соединение резисторов
При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений.
Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной.
Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.
Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация.
Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н.
«каскадом», применяются правила и формулы для последовательного соединения.
Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
Источник: https://pechi-sibiri.ru/kak-najti-silu-toka-na-kazhdom-rezistore/
Закон Ома
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
 Георг Симон Ом
Георг Симон Ом
- Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
- Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
- Формула закона Ома записывается в следующем виде:
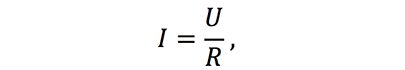
- где
- I – сила тока в проводнике, единица измерения силы тока — ампер [А];
- U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
- R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].
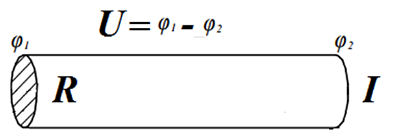
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
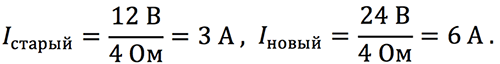
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
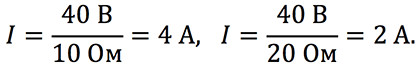
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
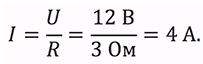
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
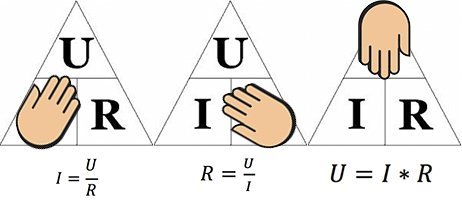
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Источник: https://zakon-oma.ru/
Закон ома
Электроника сейчас получила большое распространение, у всех дома много радиоприёмников, телефонов, компьютеров, планшетов, телевизоров фонариков и т.д. Это всё радиоэлектроника, поэтому некоторые люди заинтересовываются этим хобби, но не знают с чего начать. Наша цель рассказать в данном материале всё о Законе Ома.

Обозначения напряжения, тока, сопротивления
Всё же многие радиолюбители начинают с закона Ома. В закон Ома входят три единицы: напряжение, ток, сопротивление.
- Напряжение измеряется в вольтах (В) и обозначается U.
- Сопротивление измеряется в Омах (Ом) и обозначается R.
- Ток в Амперах (А) и обозначается I.
Расчёт напряжения, тока и сопротивления
Закон Ома предназначен для того, чтобы найти неизвестную третью, если известны первая и вторая. С этого по подробней, чтобы облегчить закон Ома, будем пользоваться треугольником Ома. Вот этот треугольник:
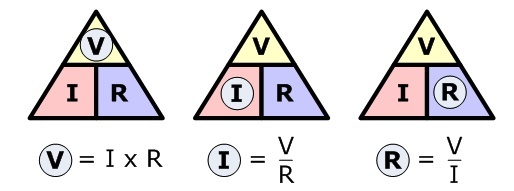
Давайте разберёмся с напряжением, чтобы найти напряжение, используя треугольник Ома, надо закрыть рукой напряжение — U, остались только I-ток и R-сопротивление, передними стоит вертикальная черта, вертикальная это черта снизу вверх, это вертикальная линия обозначает умножение, значит, чтобы найти напряжение надо ток умножить на сопротивление.
Вот такая формула получилась: U=I*R, где U-напряжение, I-ток, R-сопротивление.
Теперь давайте попробуем найти ток, прикроем рукой I, теперь перед напряжением и сопротивление стоит горизонтальная черта, горизонтальная, это та черта, которая идёт слева направо. Горизонтальная черта означает деление. Значит, чтобы найти ток, надо напряжение разделить на сопротивление.
Формула получилась следующая: I= UR, где I-ток, U-напряжение, R-сопротивление.
Найдём сопротивление, закроем рукой R, то получим опять горизонтальную черту перед напряжением и током, значит нужно делить.
Формула получилась для расчёта сопротивления: R=UI, где R-сопротивление, U-напряжение, I-ток. Итак, мы научились пользовать треугольником Ома и узнали о Законе Ома. Теперь, пожалуй, поучимся на примерах.
Примеры расчётов закона Ома
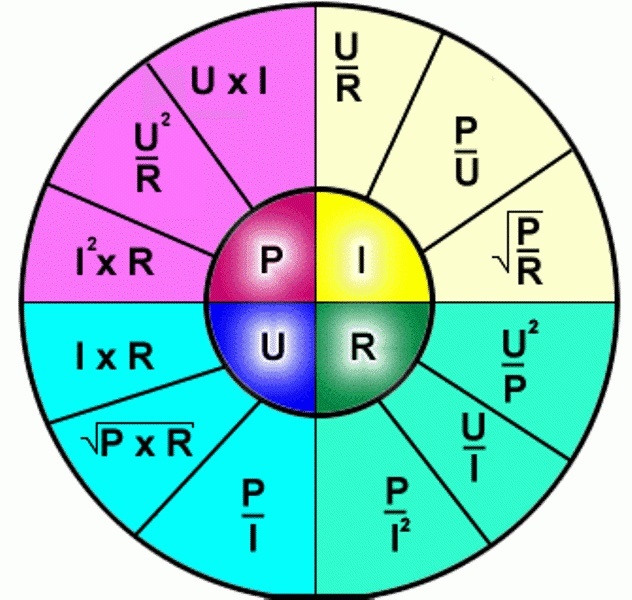
Давайте, найдём напряжение, если ток равен 0,9 Ампер, а сопротивление 100 Ом, пользуясь треугольником, прикрываем напряжение рукой, смотрим, вертикальная черта, значит умножить. Опять пользуемся той формулой, только подставляем числа, U = 0,9 А * 100 Ом, считаем, получиться 90, значит U = 90 вольт.
Теперь рассчитываем сопротивление, берём те же единицы, только убираем сопротивление, получиться вот такая формула: R = 90 В 0,9 А, получим 100 Ом.
Чтобы рассчитать ток, опять же убираем ток, получаем эту формулу I = 90 В 100 Ом, получаем 0,9 Ампер.
Итак, на этом всё, кстати, закон Ома действует там, где нет катушек индуктивности и конденсаторов, не забивайте голову конденсаторами и катушками индуктивности, просто, запомните, что закон Ома действует, там, где нет катушек индуктивности и конденсаторов. Надеюсь, моя статья была полезной, всем удачи, с вами был Дмитрий Цывцын.
Справочники радиодеталей
|
|
|
Источник: https://elwo.ru/publ/spravochniki/zakon_oma/2-1-0-898
10 формул
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике.
Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем.
К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Соотношения закона Ома
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
- В этой таблице используются следующие общепринятые обозначения физических величин:
- U — напряжение (В),
- I — ток (А),
- Р — мощность (Вт),
- R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт.
Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
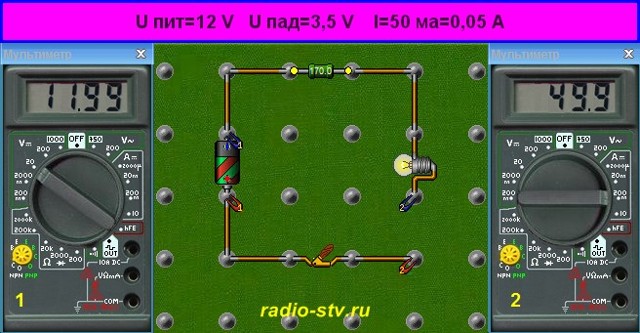
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
- > R: искомое сопротивление токоограничивающего резистора, в омах.
- В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
- R = U/I = 8,5 В / 0,050 А= 170 Ом
Расчёты сопротивления
Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторов
- Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
- Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
- В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.
- Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов
- Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов.
Формула приобретает вид:
- R общ = R1 * R2 / (R1 + R2)
- где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина.
Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
- 776,47 = 2640000 / 3400

- Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
- Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.
Расчёты ёмкости
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторов
- Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
- Собщ = CI + С2 + СЗ + …
- В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторов
- Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
- Собщ = С1 * С2 /( С1+С2)
- где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторов
В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравнений
Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Расчёт постоянной ёмкости RC-цепочки
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Расчёты частоты и длины волны
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Расчет частоты сигнала
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети.
Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны.
Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигнала
- Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
- Длина волны = 300000 / Частота
- Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
Источник: https://radio-stv.ru/nachinayushhim-radiolyubitelyam/10-formul