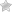Вычисляем мощность переменного и постоянного электрического тока по формуле

Мощность — то, что характеризует скорость передачи с преобразованием электроэнергии. Какие есть нормы мощности в сети переменного тока и виды, что такое активная и реактивная мощность? Об этом и другом далее.

Нормы мощности в сети переменного тока

Напряжение и мощность — то, что нужно знать каждому человеку, живущему в квартире или частном доме. Стандартное напряжение сети переменного тока в квартире и частном доме выражается в количестве 220 и 380 ватт.

Что касается определения количественной меры силы электрической энергии, необходимо сложить электрический ток с напряжением или же измерить необходимый показатель ваттметром.

При этом чтобы сделать измерения последним аппаратом, нужно использовать щупы и специальные программы.

Что такое мощность переменного тока

Мощность переменного тока определяется соотношением величины тока со временем, которая производит работу за определенное время. Обычный пользователь использует мощностный показатель, передаваемый ему поставщиком электрической энергии. Как правило, он равен 5-12 киловатт. Этих цифр хватает, чтобы обеспечить работоспособность необходимого бытового электрооборудования.

Этот показатель зависит от того, какие внешние условия поступления энергии в дом, какие поставлены ограничительные токовые устройства (автоматы или полуавтоматы), регулирующие момент поступления мощностных емкостей к потребительскому источнику. Это совершается на разных уровнях, от бытового электрощита до центрального устройства электрического распределения.

Мощностные нормы в сети переменного тока

Характеристики

Переменный ток течет по цепи и меняет свое направление с величиной. Создает магнитное поле. Поэтому его нередко называют периодическим синусоидальным переменным электротоком.

Согласно закону кривой линии, величина его меняется через конкретный промежуток времени. Поэтому он называется синусоидным. Имеет свои параметры.

Из важных стоит указать период с частотой, амплитудой и мгновенным значением.

Амплитуда — токовое максимальное значение с напряжением и эффективностью протекания на протяжении полного периода. Мгновенное значение — переменный ток или напряжение, возникающее за конкретное время.

Характеристики переменного тока

Виды мощностей

Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии.

Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N.

В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.

Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.

Основные мощностные разновидности

Активная мощность

Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.

Активная разновидность

Реактивная мощность

Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов. Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением.

Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.

Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне. Активно применяются в промышленности.

Реактивная разновидность

Полная мощность

Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.

Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.

Полная разновидность

Комплексная мощность

Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи.

Аргументом является фазовый сдвиг между электротоком с сетевым напряжением.

Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.

Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс. Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.

Комплексная разновидность

Как узнать какая мощность в цепи переменного тока

Стоит указать, что это величина, которая прямо связывается с иными показателями. К примеру, она находится в прямой зависимости от времени, силы, скорости, вектора силы и скорости, модуля силы и скорости, момента силы и частоты вращения.

Часто в формулах во время вычисления электромощности используется также число Пи с показателем сопротивления, мгновенным током, напряжением на конкретном участке электрической сети, активной, полной и реактивной силой.

Непосредственно участник вычисления это амплитуда, угловая скорость и начальная сила тока с напряжением.

Формула мощности в цепи переменного тока

В однофазной цепи

Понять, какой мощностный показатель есть в однофазной цепи переменного тока, можно при помощи применения трансформатора тока. Для этого необходимо воспользоваться ваттметром, который включен через токовый трансформатор. Показания следует перемножить на трансформаторный коэффициент тока.

В момент измерения мощности в высоком напряжении трансформатор тока необходим, чтобы заизолировать ваттметр и обеспечить безопасность пользователя. Параллельна цепь включается не непосредственным способом, а благодаря трансформатору напряжения.

Вторичные обмотки с корпусами измерительных трансформаторных установок необходимо заземлять во избежание случайного изоляционного повреждения и попадания высокого напряжения на приборы.

Обратите внимание! Для определения параметров в сети необходимо амперметр перемножить на трансформаторный коэффициент тока, а цифры, полученные вольтметром, перемножить на трансформаторный коэффициент напряжения.

В однофазной цепи

В трехфазной цепи

В цепи переменного тока мощностный показатель в трехфазной цепи определить можно, перемножив ток на напряжение. Поскольку это непостоянный электроток, он зависит от времени и других параметров, поэтому необходимо использовать другие проверенные схемы. Так, можно использовать ваттметр.

Измерение должно быть проведено только в одной фазе и по формуле умножено на три. Этот способ экономит приборы и уменьшает габариты измерения. Применяется для высокой точности измерения каждой фазы. В случае несимметричной нагрузки, нужно использовать соответствующую схему подключения ваттметра. Это более точный способ, но требует наличие трех ваттметров.

Обратите внимание! Если цепь не предусматривает наличие нулевого проводника, нужна также соответствующая схема.

Стоит указать, что сегодня измерить можно необходимые показатели не только аналоговым, но и цифровым прибором. Отличие второго в уменьшенных размерах и легкости.

Это удобно, поскольку не нужно измерять ток с напряжением, а потом, используя формулы, все досконально просчитывать.

В трехфазной цепи

В целом, мощность — это величина, основное предназначение которой показывать силу работы конкретного прибора и во многих случаях скорость деятельности, взаимодействуя с ним. Она бывает механической, электрической, гидравлической и для постоянного с переменным током. Измеряется по международной системе в ваттах и киловаттах.

Источник: https://rusenergetics.ru/polezno-znat/moschnost-peremennogo-toka

Переменный электрический ток

Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.

Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC — Direct Current — постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.

Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

• Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
• Частота  f — величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz)
• f = 1/T
• Циклическая частота  ω — угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза  ψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

1. Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
2. Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
3. i = i(t);   u = u(t)
4. Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
   Например, синусоидальный ток или напряжение можно выразить функцией:
5. i = Iampsin(ωt);   u = Uampsin(ωt)
6. С учётом начальной фазы:
7. i = Iampsin(ωt + ψ);   u = Uampsin(ωt + ψ)
8. Здесь Iamp и Uamp — амплитудные значения тока и напряжения.
9. Амплитудное значение — максимальное по модулю мгновенное значение за период.
10. Iamp = max|i(t)|;   Uamp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля. Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.

Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой Iamp (Uamp) среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока. В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы

Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.

Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному.

Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1

Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному.

Для переменного синусоидального тока или напряжения коэффициент формы KФ ≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ ≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1

Замечания и предложения принимаются и приветствуются!

Источник: https://tel-spb.ru/ac.html

Мощность переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

Мощность тока через резистор

• Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:
• Поэтому для мгновенной мощности получаем:
• (2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е.

Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

1. среднее значение квадрата синуса (или косинуса) за период равно .
2. Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

• Итак, для среднего значения мощности тока на резисторе имеем:
• (3)
• В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
• (4)
• Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
• Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

1. Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :
2. Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Мощность тока через катушку

• Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :
• Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

1. Тогда для мгновенной мощности имеем:
2. (5)
3. Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
4. В результате получим:
5. (6)
6. Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
7. (7)
8. Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице.

Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

Источник: https://ege-study.ru/ru/ege/materialy/fizika/moshhnost-peremennogo-toka/

Мощность электрического тока — Основы электроники

Обычно электрический ток сравнивают с течением жид­кости по трубке, а напряжение или разность потенциалов — с разностью уровней жидкости.

В этом случае поток воды, падающий сверху вниз, несет с собой определенное количество энергии. В усло­виях свободного падения эта энергия растрачивается беспо­лезно для человека. Если же направить падающий поток во­ды на лопасти турбины, то последняя начнет вращаться и сможет производить полезную работу.

Работа, производимая потоком воды в течение определен­ного промежутка времени, например, в течение одной секун­ды, будет тем больше, чем с большей высоты падает поток и чем больше масса падающей воды.

Точно так же и электрический ток, протекая по цепи от высшего потенциала к низшему, совершает работу. В каждую данную секунду времени будет совершаться тем больше рабо­ты, чем больше разность потенциалов и чем большее количе­ство электричества ежесекундно проходит через поперечное сечение цепи.

Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.

Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (на­пряжению) и силе тока в цепи.

• Для измерения мощности электрического тока принята еди­ница, называемая ватт (Вт).
• Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В.
• Для вычисления мощности постоянного тока в ваттах нуж­но силу тока в амперах умножить на напряжение в вольтах.
• Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы
• P = I*U. (1)
• Воспользуемся этой формулой для решения числового при­мера. Требуется определить, какая мощность электрического тока необходима для накала нити радиолампы, если напряжение накала равно 4 в, а ток накала 75 мА
• Определим мощность электрического тока, поглощаемую нитью лампы:
• Р= 0,075 А*4 В = 0,3 Вт.

Мощность электрического тока можно вычислить и другим путем. Предположим, что нам известны сила тока в цепи и сопротивление цепи, а напряжение неизвестно.

1. В этом случае мы воспользуемся знакомым нам соотноше­нием из закона Ома:
2. U=IR
3. и подставим правую часть этого равенства (IR) в формулу (1) вместо напряжения U.
4. Тогда формула (1) примет вид:
5. P = I*U =I*IR
6. или
7. Р = I2*R. (2)
8. Например, требуется узнать, какая мощность теряется в реостате сопротивлением в 5 Ом, если через него проходит ток, силой 0,5 А. Пользуясь формулой (2), найдем:
9. P= I2*R = (0,5)2*5 =0,25*5 = 1,25 Вт.
10. Наконец, мощность электрического тока может быть вычислена и в том слу­чае, когда известны напряжение и сопротивление, а сила тока неизвестна. Для этого вместо силы тока I в формулу (1) подставляется известное из закона Ома отношение U/R и тогда формула (1) приобретает следующий вид:
11. Р = I*U=U2/R (3)
12. Например, при 2,5 В падения напряжения на реостате сопро­тивлением в 5 Ом поглощаемая реостатом мощность будет равна:
13. Р = U2/R=(2,5)2/5=1,25 Вт
14. Таким образом, для вычисления мощности требуется знать любые две из величин, входящих в формулу закона Ома.
15. Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды.
16. P = A/t

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник: https://www.sxemotehnika.ru/moschnost-elektricheskogo-toka.html

Мощность постоянного и переменного электрического тока

Мощность
постоянного тока

Так
как значения силы тока и напряжения
постоянны и равны мгновенным значениям
в любой момент времени, то мощность
можно вычислить по формуле:

• Для
  пассивной линейной цепи, в которой
  соблюдается закон
  Ома,
  можно записать:
• ,
  где  — электрическое
  сопротивление.
• Если
  цепь содержит источник ЭДС,
  то отдаваемая им или поглощаемая на нём
  электрическая мощность равна:
• ,
  где  —
  ЭДС.

Если
ток внутри ЭДС противонаправлен градиенту
потенциала (течёт внутри ЭДС от плюса
к минусу), то мощность поглощается
источником ЭДС из сети (например, при
работе электродвигателя или
заряде аккумулятора),
если сонаправлен (течёт внутри ЭДС от
минуса к плюсу), то отдаётся источником
в сеть (скажем, при работегальванической
батареи или генератора).
При учёте внутреннего
сопротивления источника
ЭДС выделяемая на нём мощность  прибавляется
к поглощаемой или вычитается из
отдаваемой.

Мощность
переменного тока[править | править
вики-текст]

В
цепях переменного тока формула для
мощности постоянного тока может быть
применена лишь для расчёта мгновенной
мощности, которая сильно изменяется во
времени и для практических расчётов
бесполезна.

Прямой расчёт среднего
значения мощности требует интегрирования
по времени. Для вычисления мощности в
цепях, где напряжение и ток изменяются
периодически, среднюю мощность можно
вычислить, интегрируя мгновенную
мощность в течение периода.

На практике
наибольшее значение имеет расчёт
мощности в цепях переменного синусоидального
напряжения и тока.

Можно считать, что мощность в цепи
переменного тока выражается комплексным
числом таким, что активная мощность
является его действительной частью,
реактивная мощность — мнимой частью,
полная мощность — модулем, а
угол 

gIcG/img-wJNMYs.png» width=»13″> (сдвиг
фаз) — аргументом. Для такой модели
оказываются справедливыми все выписанные
ниже соотношения.

Активная
мощность[править | править
вики-текст]

Единица
измерения — ватт (W, Вт).

Среднее
за период  значение
мгновенной мощности называется активной
мощностью: .
В цепях однофазного синусоидального
тока 

png» width=»138″>,
где  и  — среднеквадратичные
значения напряжения и тока,  — угол
сдвига фаз между
ними.

Для цепей несинусоидального тока
электрическая мощность равна сумме
соответствующих средних мощностей
отдельных гармоник. Активная мощность
характеризует скорость необратимого
превращения электрической энергии в
другие виды энергии (тепловую и
электромагнитную).

Активная мощность
может быть также выражена через силу
тока, напряжение и активную составляющую
сопротивления цепи  или
её проводимость  по
формуле .

В любой электрической цепи как
синусоидального, так и несинусоидального
тока активная мощность всей цепи равна
сумме активных мощностей отдельных
частей цепи, для трёхфазных
цепейэлектрическая
мощность определяется как сумма мощностей
отдельных фаз. С полной мощностью 

png» width=»12″> активная
связана соотношением .

1. В
   теории длинных
   линий (анализ
   электромагнитных процессов в линии
   передачи, длина которой сравнима с
   длиной электромагнитной волны) полным
   аналогом активной мощности является
   проходящая мощность, которая определяется
   как разность между падающей мощностью
   и отраженной мощностью.
2. Реактивная
   мощность[править | править
   вики-текст]
3. Единица
   измерения — вольт-ампер реактивный
   (var, вар)

Реактивная
мощность — величина, характеризующая
нагрузки, создаваемые в электротехнических
устройствах колебаниями энергии
электромагнитного поля в цепи
синусоидального переменного тока, равна
произведению среднеквадратичных
значений напряжения 

png» width=»15″> и
тока ,
умноженному на синус угла сдвига
фаз  между
ними: 

png» width=»136″> (если
ток отстаёт от напряжения, сдвиг фаз
считается положительным, если опережает —
отрицательным). Реактивная мощность
связана с полной мощностью  и
активной мощностью 

png» width=»15″> соотношением: .

Физический
смысл реактивной мощности — это
энергия, перекачиваемая от источника
на реактивные элементы приёмника
(индуктивности, конденсаторы, обмотки
двигателей), а затем возвращаемая этими
элементами обратно в источник в течение
одного периода колебаний, отнесённая
к этому периоду.

Необходимо
отметить, что величина  для
значений  от
0 до плюс 90° является положительной
величиной. Величина 

gIcG/img-ounvKf.png» width=»40″> для
значений  от
0 до −90° является отрицательной величиной.
В соответствии с формулой 

Данное
обстоятельство подчёркивает тот факт,
что реактивная мощность не участвует
в работе электрического тока.

Когда
устройство имеет положительную реактивную
мощность, то принято говорить, что оно
её потребляет, а когда отрицательную —
то производит, но это чистая условность,
связанная с тем, что большинство
электропотребляющих устройств
(например, асинхронные
двигатели),
а также чисто активная нагрузка,
подключаемая через трансформатор,
являются активно-индуктивными.

Синхронные
генераторы, установленные на электрических
станциях, могут как производить, так и
потреблять реактивную мощность в
зависимости от величины тока возбуждения,
протекающего в обмотке ротора генератора.

За счёт этой особенности синхронных
электрических машин осуществляется
регулирование заданного уровня напряжения
сети.

Для устранения перегрузок и
повышения коэффициента
мощности электрических
установок осуществляется компенсация
реактивной мощности.

• Применение
  современных электрических измерительных
  преобразователей на микропроцессорной
  технике позволяет производить более
  точную оценку величины энергии
  возвращаемой от индуктивной и емкостной
  нагрузки в источник переменного
  напряжения.
• Полная
  мощность
• Единица
  полной электрической
  мощности — вольт-ампер (V·A, В·А)
• Полная
  мощность — величина, равная произведению
  действующих значений периодического
  электрического тока  в
  цепи и напряжения  на
  её зажимах: ;
  связана с активной и реактивной мощностями
  соотношением:  где  —
  активная мощность,  —
  реактивная мощность (при индуктивной
  нагрузке ,
  а при ёмкостной ).

Полная
мощность имеет практическое значение,
как величина, описывающая нагрузки,
фактически налагаемые потребителем на
элементы подводящей электросети
(провода, кабели, распределительные
щиты, трансформаторы, линии
электропередачи),
так как эти нагрузки зависят от
потребляемого тока, а не от фактически
использованной потребителем энергии.
Именно поэтому полная мощность
трансформаторов и распределительных
щитов измеряется в вольт-амперах, а не
в ваттах.

1. Комплексная
   мощность[править | править
   вики-текст]
2. Мощность,
   аналогично импедансу,
   можно записать в комплексном виде:
3.  где  —
   комплексное напряжение,  —
   комплексный ток,  —
   импеданс, * — оператор комплексного
   сопряжения.

Модуль
комплексной мощности  равен
полной мощности .
Действительная часть 

png» width=»50″> равна
активной мощности ,
а мнимая  —
реактивной мощности 

png» width=»15″> с
корректным знаком в зависимости от
характера нагрузки.

Источник: https://studfile.net/preview/6018855/page:4/