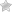Определение и использование эффекта холла: аномальный, квантовый и спиновый эффекты

Принцип эффекта Холла — одна из самых популярных теорий измерения магнитного поля. В этом посте будут обсуждаться Эффект Холла, принцип его работы, объяснение теории, формула, применение, включая расчеты для напряжения Холла, коэффициента Холла, концентрации носителей заряда, подвижности Холла и плотности магнитного поля.

Принцип эффекта Холла объясняет поведение носителей заряда при воздействии электрического и магнитного полей. Этот принцип можно рассматривать как расширение силы Лоренца, которая является силой, действующей на носители заряда (электроны и отверстия), проходящие через магнитное поле.

Датчики, работающие по этому принципу, называются датчиками Холла. Эти датчики Холла пользуются большим спросом и имеют очень широкое применение, например, датчики приближения, переключатели, датчики скорости вращения колес, датчики положения и так далее.

История эффекта Холла

Принцип эффекта Холла был назван в честь американского физика Эдвина Холла (1855–1938). Впервые он был представлен миру в 1879 году.

В 1879 году он обнаружил, что когда проводник / полупроводник с током расположен перпендикулярно магнитному полю, генерируется напряжение, которое можно измерить под прямым углом к ​​пути тока. В течение этого времени электрический ток в проводе считался чем-то похожим на текущую жидкость в трубе.

Принцип эффекта Холла предполагает, что магнитная сила в токе приводит к скученности на конце трубы или (провода).

 Электромагнитный принцип теперь объясняет науку, лежащую в основе эффекта Холла, гораздо лучше. Теория этого зала, безусловно, намного опередила свое время.

 Лишь два десятилетия спустя, с введением полупроводников, работа и использование эффекта Холла были эффективно использованы.

Первоначально этот принцип использовался для классификации химических образцов.

 Позднее датчики Холла (с использованием полупроводниковых соединений арсенида индия) стали источником для измерения постоянного или статического магнитного поля, не поддерживая датчик в движении.

 После десятилетия в 1960-х годах появились кремниевые полупроводники. Это было время, когда элементы Холла были объединены со встроенными усилителями, и таким образом, выключатель Холла был представлен миру.

Принцип работы эффекта Холла

Принцип эффекта Холла гласит, что когда проводник или полупроводник с током, текущим в одном направлении, вводится перпендикулярно магнитному полю, напряжение может быть измерено под прямым углом к ​​пути тока.

Эффект получения измеримого напряжения, как сказано выше, называется эффектом Холла.

Теория за принципом эффекта Холла

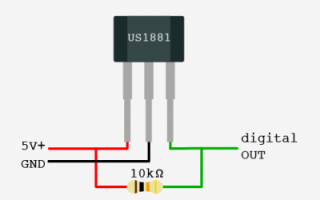
Прежде всего, мы должны понять, что такое электрический ток. Электрический ток — это в основном поток заряженных частиц через проводящий путь. Эти заряженные частицы могут быть «отрицательно заряженными электронами» или даже «положительно заряженными отверстиями» (пустоты, в которых должны находиться электроны). Теперь давайте перейдем к теме.

Если мы возьмем тонкую проводящую пластину (как показано выше на рис. 1 и повторено ниже для простоты считывания) и подключим ее к цепи с батареей (источником напряжения), то ток начнет течь по ней. Носители заряда будут течь по прямой линии от одного конца пластины к другому концу.

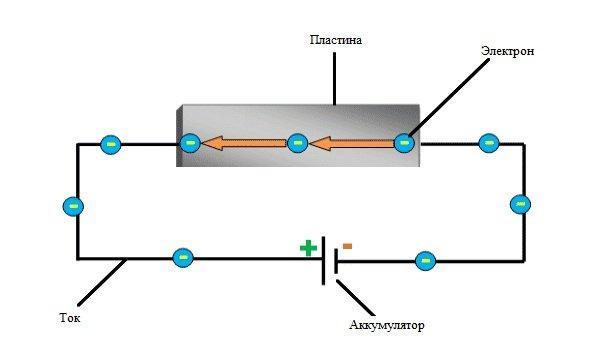
Поскольку носители заряда находятся в движении, они будут создавать магнитное поле. Теперь, когда вы поместите магнит рядом с пластиной, его магнитное поле будет искажать магнитное поле носителей заряда. Это расстроит прямой поток носителей заряда. Сила, которая нарушает направление потока носителей заряда, называется силой Лоренца.

Из-за искажения в магнитном поле носителей заряда отрицательные заряженные электроны будут отклоняться на одну сторону пластины, а положительные заряженные дыры — на другую сторону. Вот почему разность потенциалов (также называемая напряжением Холла) будет генерироваться между обеими сторонами пластины, что можно измерить с помощью измерителя.

Этот эффект известен как эффект Холла. Чем сильнее магнитное поле, тем больше электронов будет отклоняться. Это означает, что чем выше ток, тем больше электронов будет отклоняться. И чем больше будут отклоняться электроны, тем больше будет разность потенциалов между обеими сторонами пластины. Поэтому мы можем сказать, что:

• Напряжение Холла прямо пропорционально электрическому току, и прямо пропорционально приложенному магнитному полю.

Формула эффекта Холла

Вот некоторые математические выражения, которые широко используются в вычислениях эффекта Холла:

Напряжение Холла

Напряжение Холла представлена V H. Формула для напряжения Холла:

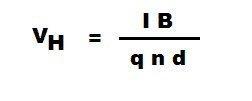
• Где:
• I — Ток, протекающий через датчик
• B — напряженность магнитного поля
• q — заряд
• n — количество носителей заряда на единицу объема
• d — толщина датчика

Коэффициент Холла

Оно представлено RH. Формула для коэффициента Холла (R H ) равно 1 / (qn) . Коэффициент Холла (R H ) положителен, если число отверстий положительного заряда больше, чем число электронов отрицательного заряда. Аналогично, коэффициент Холла (RH) отрицателен, если число отрицательных зарядовых электронов больше, чем число отверстий положительного заряда.

Концентрация несущей заряда

Концентрация электронов в носителе заряда обозначена как «n», а «дырки» — как «p». Математическое выражение для концентрации носителей заряда:

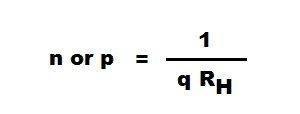
Холловская  мобильности

Холловская мобильность для электронов представлена ​​как « μ n », а для отверстий — как « μ p ». Математическое выражение для мобильности Холла:

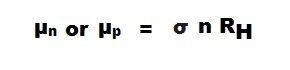
1. Где:
2. μ n — проводимость за счет электронов
3. μ p — проводимость благодаря отверстиям

Плотность магнитного потока

Плотность магнитного потока обозначена буквой «B». Формула для плотности магнитного потока:

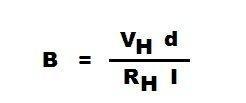
Применение принципа эффекта Холла

Принцип эффекта Холла используется в:

• Оборудование для измерения магнитного поля.
• Множитель приложений для обеспечения фактического умножения.
• Тестер Эффекта Холла для измерения постоянного тока.
• Измерение фазового угла. Например — при измерении углового положения коленчатого вала, чтобы точно выровнять угол зажигания свечей зажигания
• Датчики линейных или угловых перемещений. Например — определить положение автомобильных сидений и ремней безопасности и выступить в роли блокировки для управления подушкой безопасности.
• Датчики приближения.
• Датчики с эффектом Холла
• Для определения скорости вращения колеса и, соответственно, помощи антиблокировочной тормозной системы (ABS).

Как эффект Холла можно использовать для определения типа используемого полупроводника?

Коэффициент Холла говорит обо всем. Если коэффициент Холла отрицателен, это означает, что основными носителями заряда являются электроны.

 И поскольку число электронов больше по сравнению с отверстиями в полупроводниках n-типа, это ясно указывает на то, что испытываемый полупроводник n-типа. Аналогичным образом, если коэффициент Холла положительный, это означает, что основными носителями заряда являются дырки.

 И поскольку число отверстий больше по сравнению с электронами в полупроводниках p-типа, это ясно указывает на то, что испытываемый полупроводник p-типа.

Источник: https://meanders.ru/jeffekta-holla-princip-raboty-objasnenie-teorii-formula.shtml

Эффект холла — в чем заключается, применение для датчиков тока и положения, формула, квантовый, аномальный и другие виды

Электричество и магнитные поля существуют в тесной взаимосвязи друг с другом.

Многие известные физики посвятили жизнь исследованию этой связи, поиску и описанию законов, на которых она базируется, а также способов применения на практике полученных теоретических сведений.

Одним из таких учёных был Эдвин Герберт Холл, выдающийся американский исследователь, автор ценных научных материалов. В ходе одного из экспериментов он обнаружил необычное явление, которое со временем получило название «эффект Холла».

Сегодня он массово используется в бытовой и компьютерной технике, электрооборудовании автомобилей, контрольно-измерительных приборах и, конечно, исследовательских лабораториях. Так в чём же физическая суть эффекта Холла и почему он не теряет своей актуальности спустя почти полтора века с момента открытия?

Что такое эффект Холла?

Эдвин Холл, пропуская ток через тонкую золотую пластину, расположенную между двумя магнитами, заметил, что носители заряда (электроны) отклоняются от центральной оси к одной из граней проводника.

Таким образом, на этой грани возникает отрицательный заряд, а на противоположной — положительный. Возникшая разность потенциалов именуется холловским напряжением. Она строго перпендикулярна току в проводнике и вектору магнитной индукции.

Это явление наблюдается не только в золоте, но и в любых проводниковых и полупроводниковых материалах, помещённых в магнитное поле.

Если проанализировать физическую суть, можно обнаружить, что у истоков накопления заряда на гранях проводника лежит сила Лоренца, с которой магнитное поле воздействует на заряженную частицу. Под её воздействием электроны будут накапливаться на грани проводника до тех пор, пока их суммарный заряд не скомпенсирует существующее магнитное поле.

В том же случае, когда внешнее магнитное поле слишком велико, система выйдет за рамки стабильности, и заряженные частицы начнут двигаться по циклоиде. Это называется несоблюдением критерия малости.

Виды

Цифровые датчики Холла делятся на униполярные и биполярные

Помимо эффекта Холла, законы которого описаны классической физикой и соблюдаются во всех нормальных или приближённых к нормальным условиям экспериментах, выделяют ещё несколько разновидностей явления возникновения разности потенциалов в проводнике.

Аномальный

Аномальным называют любой случай накопления заряда на грани проводника, в котором исключено воздействие внешних магнитных полей. Необходимым условием является перпендикулярная направленность разницы потенциалов относительно направления силы тока.

Причины, по которым возникает аномальный эффект Холла, обычно кроются в намагниченности металла-проводника или особенностях его молекулярной структуры.

Квантовый

Законы возникновения разницы потенциалов в «квантовом мире» исследуются на примере плоского проводника типа ДЭГ (двумерный электронный газ).

Квантовый наблюдается в сильных магнитных полях и при низких температурах. Он выражается в квантовании холловского сопротивления, которое на графике имеет чётко выраженные «участки плато».

Чем выше сопротивление, тем длиннее участки плато и выше разница между ними.

Открытие данного явления — одна из основных вех современной квантовой физики. Клаус фон Клитцинг, первооткрыватель квантового эффекта Холла, в 1985 году был удостоен Нобелевской премии.

Дробный

Многие передовые учёные в 80-х годах прошлого века заинтересовались исследованиями фон Клитцинга и продолжили изучать свойства разности потенциалов в ДЭГ.

Наибольших успехов достигли Даниэль Цуи и Хорст Штёрмер, которые проанализировали промежуточные участки между «плато сопротивления» и пришли к выводу, что при существенном увеличении интенсивности магнитных полей «участки плато» можно получить и на дробных значениях электронных уровней Ландау, например, при n=1/3; n=2/5; n=3/7 и т. д.

Такое явление получило название дробного квантового эффекта Холла, а его первооткрыватели получили Нобелевскую премию по физике в 1998 году. В настоящее время ведутся расширенные исследования квантового и дробного квантового видов данного эффекта.

Спиновый

В 2003–2004 годах было изучено поведение электронов с антипараллельными спинами в проводниках, изолированных от каких-либо магнитных полей.

Теоретической базой исследования послужили теории Владимира Переля, выдвинутые в далёком 1971 году.

Они были доказаны на практике, когда удалось зафиксировать отклонения данных групп электронов к противоположным граням проводника. Движение заряженных частиц напоминает первый вид эффекта — аномальный.

Формулы и расчёты

Поскольку данный эффект базируется на силе Лоренца, то именно с её определения и начинается математическое описание возникшей разницы потенциалов. Сила Лоренца определяется из следующего выражения:

Fл=qvB, где:

• q — заряд частицы;
• v — скорость движения частиц;
• B — внешнее магнитное поле.

Электрическое поле, сформированное образовавшимися на гранях проводника зарядами, тоже влияет на движущиеся в сечении электроны. Сила этого влияния описывается так:

Fэл=qE, где:

• q — заряд частицы;
• E — напряжённость внутреннего электрического поля.

Когда разность потенциалов уравновешивает магнитное поле, система считается стабильной. При этом соблюдается условие Fл= Fэл. Следовательно, верны и два следующих утверждения:

• qvB= qE
• E=vB
• Скорость электронов обычно определяется с помощью формулы плотности тока:
• j=qnv; v=j/qn, где:

• q — заряд частицы;
• n — кол-во частиц на единицу объёма.

1. Теперь электрическое поле E можно описать с помощью выражения:
2. E=jB/qn
3. Найдём разность потенциалов:
4. Uн=dE=djB/qn, где d — толщина проводящей пластины.
5. Упростить данное выражение можно с помощью так называемой «постоянной Холла», которая имеет вид R=1/qn. Окончательная формула разности потенциалов примет вид:
6. Uн=RdjB
7. То есть, разность потенциалов прямо пропорциональна толщине проводника, магнитной индукции и плотности тока.

Применение

Поскольку данное явление позволяет адекватно оценить концентрацию и подвижность заряженных частиц, проследить чёткую зависимость между силой тока, внешним магнитным полем и поведением электронов в материале, он нашёл широкое применение на практике. В общем виде устройства и приборы, принцип действия которых основан на эффекте Холла, можно разделить на две категории: контрольно-измерительное оборудование для материалов с различной проводимостью и электронные датчики.

В проводниках и полупроводниках

В точном машиностроении рассматриваемый эффект используют для определения электромагнитных свойств и молекулярной структуры материала.

В проводниках эти показатели оцениваются посредством анализа движения электронов под воздействием силы тока и магнитных полей, в полупроводниках же с равной эффективностью анализируется как поведение электронов, так и образование электронных дырок. Широкое распространение получил метод ван дер Пау, позволяющий определить:

• тип полупроводника (p или n);
• концентрацию заряженных частиц;
• холловскую подвижность заряженных частиц.

Метод применим к любому плоскому образцу произвольной формы, толщина которого намного меньше длины исследуемого участка. Он широко используется при первичных расчётах полупроводниковых приборов: диодов, транзисторов, тиристоров и др.

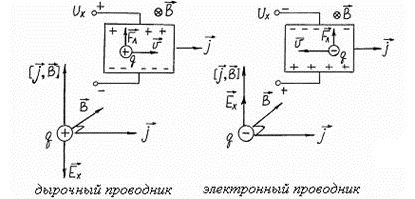
Направление поля Холла в проводниках зависит от их типа

Датчики Холла — назначение и разновидности

Самостоятельные устройства и элементы систем, использующие интересующий нас эффект для измерения магнитоэлектрических величин, называют датчиками Холла. Их делят на две большие группы: аналоговые и цифровые.

Аналоговые датчики очень просты и представляют собой, как правило, изолированный источник магнитного поля, действие которого на проводник напрямую зависит от расстояния и полярности.

Такие датчики служат для преобразования магнитной индукции в разность потенциалов.

Они необходимы для измерения магнитных полей. Если индукция поля превышает заданный порог срабатывания датчика, то он формирует цифровой сигнал «1», в противном случае значение сигнала – «0». Ввиду наличия «слепых зон», в которых индукция слишком мала для срабатывания датчика, его применение не всегда целесообразно. Цифровые датчики холла делят на:

• униполярные — генерируют выходной сигнал в магнитном поле любой полярности, отключаются при падении индукции;
• биполярные — переключают выходной сигнал с «1» на «0» при изменении полярности магнитного поля.

Датчики Холла встречаются в почти любой достаточно сложной электронике — от бесконтактных выключателей до смартфонов, от автомобильных двигателей до ионных двигателей космических кораблей.

Способность реагировать на появление и изменение магнитных полей сделала устройство незаменимым в электронике и электромеханике, а отсутствие прямого физического взаимодействия обеспечило высокую надёжность и точность, износостойкость и долговечность датчиков.

Изготовление датчика тока на основе эффекта Холла

Если Вы обладаете хотя бы базовыми навыками в работе с электронными компонентами, то без особого труда сможете самостоятельно сконструировать датчик тока. С его помощью можно будет бесконтактно определять наличие электрического тока в проводнике. Вот полный перечень материалов и инструментов, которые Вам понадобятся:

• цифровой датчик Холла в «транзисторном» корпусе, например, A3144 или US1881;
• ферритовое кольцо внешним диаметром не менее 25 мм (можно купить в магазине радиодеталей или извлечь из старого блока питания от энергосберегающих ламп или ПК);
• электрический зажим типа «крокодил»;
• цианакрилатный клей;
• резистор и конденсатор номиналами соответственно 10 кОм и 0,1 мкФ;
• плата Arduino, макетная плата, провода — для временной макетной сборки;
• плата Arduino, припой, канифоль, паяльник, провода — для сборки навесным монтажом;
• ручной лобзик с набором пилок, надфили, наждачная бумага, кусочки резины или ветоши.

Разверните корпус датчика маркировкой к себе. Нумерация выводов слева направо классическая: 1, 2, 3. Между первой и второй ножкой установите керамический конденсатор ёмкостью 0,1 мкФ (100 нФ). Между первой и третьей ножкой установите резистор сопротивлением 10 кОм. Теперь подключим датчик к плате Arduino по такой схеме:

• «1» — к контакту 5V+;
• «2» — к контакту GND;
• «3» — к цифровому выходу.

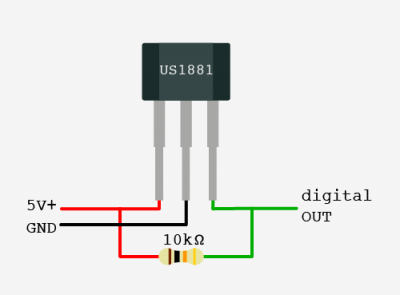
Устанавливать кермачиеский конденсатор между первой и второй ножками необязательно, но рекомендуется для стабилизации входящего напряжения

Ферритовое кольцо аккуратно распилите пополам с помощью ручного лобзика. Материал твёрдый, но достаточно хрупкий, поэтому работать придётся осторожно.

Полученные полукольца очистите от сколов и шероховатостей, после чего приклейте сбоку к «челюстям» зажима-крокодила так, чтобы в сжатом состоянии торцы полуколец едва касались друг друга.

На один из торцов наклейте кусочек плотной толстой ткани или резины, на второй — корпус цифрового датчика Холла.

Теперь, поместив внутри разрезанного ферритового кольца проводник и пустив по нему электрический ток, вы сможете наблюдать появление входящего сигнала на плате Arduino.

На сегодняшний день классический эффект Холла полностью изучен и служит теоретической базой для более или менее сложных электронных устройств. Ведутся исследования частных разновидностей эффекта Холла, в том числе поиск способов их использования в электрических, жидко- и газотопливных двигателях нового поколения.

Источник: https://elektro.guru/osnovy-elektrotehniki/effekt-holla.html

Эффект Холла и его применение

После проведения эксперимента в 1879 году Эдвином Холлом при пропускании магнитного потока через тонкую пластину из золота было обнаружено возникновение на краях пластины разности потенциалов, то есть образовался эффект Холла.

В чем заключается эффект холла

Определение 1

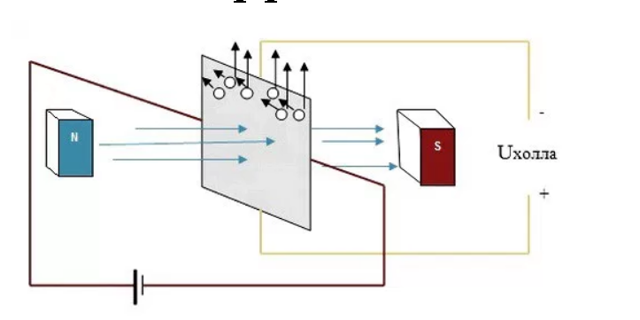
При помещении в магнитное поле пластины-проводника или полупроводника под 90 °к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

Это можно рассмотреть на простейшем примере.

Пример 1

Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.

Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным.

Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный.

Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.

При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.

Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.

Определение 2

Uхолл=-IBet, где I является силой тока, B – вектором магнитной индукции, e – зарядом электрона, p – количеством электронов в единице объема, t – толщиной пластины.

Аномальный ЭХ

Имеются случаи, когда ЭХ может быть обнаружен в пластине без пропускания через нее магнитного потока. Это возможно при нарушении симметрии по отношению к обращению времени в системе. В частности, аномальный ЭХ способен проявляться в намагниченных материалах.

Квантовый ЭХ

Двумерные газы со средним расстоянием между частицами, уменьшенным до значения длины де Бройля на зависимости поперечного сопротивления к воздействию магнитного поля, подвержены возникновению плато сопротивления в поперечине. ЭХ квантуется только в сильных магнитных полях.

Магнитные потоки, обладающие больше силой индукции, имеют дробный квантовый ЭХ. Он взаимосвязан с перестроением внутренней структуры двумерной электронной жидкости.

Спиновый ЭХ

СЭХ можно наблюдать на не намагниченных проводниках, которые не переместили в поле действия силовых линий магнита. Суть эффекта – отклонение электронов с антипараллельными спинами к противоположным краям пластины.

Применение эффекта Холла

Применение метода Холла связано с изучением особенностей полупроводников. С его помощью стало возможным вычисление количества носителей заряда на единицу объема, а также их подвижность. При его использовании реально отличить электрон от квазичастицы с положительным зарядом.

ЭХ всегда считался основой для разработки датчиков Холла. Аппаратура предназначена для измерения напряженности магнитного поля. Их используют для построения моторов со следящим приводом. В моторах они исполняют роль датчика обратной связи. Они способны измерить угол поворота вала мотора.

Датчики Холла устанавливают в электростартерах ДВС, охлаждающих системах ПК, навигационных системах мобильных телефонов, в измерительных приборах для вычисления количества заряда.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Источник: https://Zaochnik.com/spravochnik/fizika/magnitnoe-pole/effekt-holla/

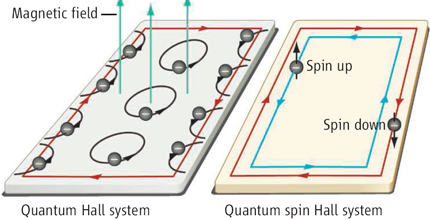
Квантовый спиновый эффект Холла

Спиновый эффект Холла был давно предсказан теоретиками и недавно наблюдался в эксперименте. Для спинового эффекта Холла не требуется внешнее магнитное поле.

Отличают два типа этого эффекта: внутренний и внешний. Внешний эффект возникает в результате анизотропии рассеяния электронов на кулоновских центрах, вызванной спин-орбитальным взаимодействием.

При протекании тока электроны со спином вверх относительно плоскости преимущественно рассеиваются направо, а электроны со спином вниз – налево. На боковых краях возникает избыток электронов со спином вверх и со спином вниз аналогично избыточному заряду в обычном эффекте Холла.

Внутренний спиновый эффект Холла обусловлен анизотропией движения электронов с различной ориентацией спина в кристалле.

После обнаружения классического спинового эффекта Холла сразу возник вопрос, не существует ли квантовый спиновый эффект Холла (QSHE), аналогичный знаменитому квантовому эффекту Холла (QHE). Возможная аналогия демонстрируется рисунком.

В режиме QHE, когда несколько подзон Ландау полностью заполнены, и наблюдается ступенька на холловском токе, вдоль краев структуры течет незатухающий (persistent) зарядовый ток. Отсутствие затухания вызвано тем, что для этого электроны должны перейти в верхние подзоны Ландау, для чего им надо преодолеть энергетический зазор.

В режиме QSHE вдоль краев должен возникать незатухающий спиновый ток. Аналогия на этом прекращается, поскольку заряд является квантованной величиной, а проекция спина – величиной непрерывной.

Как все-таки можно было бы добиться незатухающего спинового тока? Ведь его существование могло бы оказаться хорошей находкой для спинтроники.

Ясно, что этот эффект не может быть обусловлен внешним спиновым эффектом Холла, поскольку рассеяние на примесях неизбежно приводит к диссипации.

Одного внутреннего механизма недостаточно, надо обеспечить сохранение спина при протекании спинового тока, чтобы все-таки выйти на аналогию с обычным QHE. Теоретики предложили использовать новое состояние материи – спиновый изолятор.

Это состояние может возникать в результате спин-орбитального взаимодействия, приводящего к возникновению запрещенной зоны. Возможно, переход к такому состоянию происходит в гетероструктурах узкозонных полупроводников, например, CdTe/HgTe/CdTe. В режиме спинового изолятора нижняя зона заполнена электронами только с одной ориентацией спина, а до другой зоны имеется щель.

Зарядовый ток течь не может, а вот спиновый ток – может, причем, незатухающий. В недавнем эксперименте König et al. (Universität Würzburg) [2] удалось наблюдать некоторые намеки на существование спинового изолятора и рассмотренных краевых состояний в спиновом эффекте Холла.

Автор – В. Вьюрков

• 1. N. Nagaosa, Science 318, 758 (2007)
• 2. N. Nagaosa, Science 318, 758 (2007)

Пожалуйста, оцените статью:

Источник: https://www.NanoNewsNet.ru/news/2008/kvantovyi-spinovyi-effekt-kholla-0

Аномальный эффект Холла

Случай
появления напряжения (электрического
поля) в образце, перпендикулярного
направлению пропускаемого через
образец тока,
наблюдающегося в отсутствие приложенного
постоянного магнитного
поля (то
есть явление, полностью аналогичное
эффекту Холла, но наблюдающееся без
внешнего постоянного магнитного поля),
называется аномальным
эффектом Холла.

Необходимым
условием для наблюдения аномального
эффекта Холла является нарушение инвариантности
по отношению к обращению времени в
системе. Например, аномальный эффект
Холла может наблюдаться в образцах
с намагниченностью[2].

[Править]Квантовый эффект Холла

Основная
статья:Квантовый
эффект Холла

В
сильных магнитных полях в
плоском проводнике (то
есть в квазидвумерном
электронном газе)
в системе начинают сказываться квантовые эффекты,
что приводит к появлению квантового
эффекта Холла: квантованию холловского
сопротивления. В ещё более сильных
магнитных полях проявляется дробный
квантовый эффект Холла,
который связан с кардинальной перестройкой
внутренней структуры двумерной электронной
жидкости.

[Править]Спиновый эффект Холла

Основная
статья:Спиновый
эффект Холла

В
случае отсутствия магнитного поля в
немагнитных проводниках может наблюдаться
отклонение носителей тока с противоположными
направлениями спинов в разные стороны
перпендикулярно электрическому полю.

Это явление, получившее название
спинового эффекта Холла, было теоретически
предсказано Дьяконовым и Перелем в 1971
году. Говорят о внешнем и внутреннем
спиновых эффектах.

Первый из них связан
со спин-зависимым рассеянием, а второй
— со спин-орбитальным
взаимодействием.

Применение

Датчик
Холла, используемый для измерения силы
тока в проводнике. В отличие от
трансформатора тока, измеряет также и
постоянный ток.

Эффект
Холла, в некоторых случаях, позволяет
определить тип носителей заряда
(электронный или дырочный)
в металле илиполупроводнике,
что делает его достаточно хорошим
методом исследования свойств
полупроводников.

На
основе эффекта Холла работают датчики
Холла: приборы, измеряющие напряжённость
магнитного поля.
Датчики Холла получили очень большое
распространение в бесколлекторных,
или вентильных, электродвигателях
(сервомоторах).

Также
на основе эффекта Холла работают
некоторые виды ионных
реактивных двигателей.

30. Закон Био-Савара-Лапласа

Магнитное
поле постоянных токов различной формы
исследовалось французскими учеными Ж.
Био (1774—1862) и Ф. Саваром (1791—1841). Результаты
их опытов были обобщены французским
ученым П. Лапласом.  Закон
Био-Савара-Лапласа для
проводника с током I, элемент dl которого
создает в некоторой точке А (рис.

1)
индукцию поля dB,
равен 

png» width=»101″> (1)  где
dl —
вектор, по модулю равный длине dl элемента
проводника и совпадающий по направлению
с током, r —
радиус-вектор, который проведен из
элемента dl проводника
в точку А поля, r — модуль радиуса-вектора r.
Направление dB перпендикулярно
dl и r,
т. е.

перпендикулярно плоскости, в которой
они лежат, и совпадает с направлением
касательной к линии магнитной индукции.
Это направление может быть найдено по
правилу правого винта: направление
вращения головки винта дает направление
dB,
если поступательное движение винта
совпадает с направлением тока в
элементе.

  Модуль
вектора dB задается
выражением   (2)  где
α — угол между векторами dl и r.

  Аналогично
электрическому, для магнитного поля
выполняется принцип
суперпозиции:
магнитная индукция результирующего
поля, создаваемого несколькими токами
или движущимися зарядами, равна векторной
сумме магнитных индукций складываемых
полей, создаваемых каждым током или
движущимся зарядом в
отдельности:   (3)  Используя
данные формулы для расчет характеристик
магнитного поля (В и Н)
в общем случае достаточно сложен. Однако
если распределение тока имеет какую-либо
симметрию, то применение закона Био —
Савара — Лапласа совместно с принципом
суперпозиции дает возможность просто
рассчитать некоторые поля. Рассмотрим
два примера.  1. Магнитное
поле прямого тока —
тока, текущего по тонкому прямому
бесконечному проводу (рис. 2). 

В
произвольной точке А, удаленной на
расстояние R от оси проводника, векторы
dB от
всех элементов тока имеют одинаковое
направление, которое перпендикулярно
плоскости чертежа («к вам»). Значит,
сложение всех векторов dB можно
заменить сложением их модулей.

За
постоянную интегрирования возьмем угол
α (угол между векторами dl и r)
и выразим через него все остальные
величины. Из рис. 2 следует, что    (радиус
дуги CD вследствие малости dl равен
r, и угол FDC по этой же причине можно
считать прямым).

png» width=»264″>  Значит,
магнитная индукция поля прямого
тока   (5)  2. Магнитное
поле в центре кругового проводника с
током (рис.
166). Как видно из рисунка, каждый элемент
кругового проводника с током создает
в центре магнитное поле одинакового
направления — вдоль нормали от витка.

Значит, сложение векторов dB также
можно заменить сложением их модулей.
Поскольку расстояние всех элементов
проводника до центра кругового тока
одинаково и равно R и все элементы
проводника перпендикулярны радиусу-вектору
(sinα=1), то, используя
(2),    Тогда 

lFOd/img-cmU04w.png» width=»335″>  Следовательно,
магнитная индукция поля в центре
кругового проводника с током   

Рис.3

31. Закон Био-Савара-Лапласа и применение
его к расчёту магнитного поля прямолинейного
проводника стоком.

В
произвольной точке А, удаленной на
расстояние R от оси проводника, векторы
dB от
всех элементов тока имеют одинаковое
направление, которое перпендикулярно
плоскости чертежа («к вам»). Значит,
сложение всех векторов dB можно
заменить сложением их модулей.

За
постоянную интегрирования возьмем угол
α (угол между векторами dl и r)
и выразим через него все остальные
величины. Из рис. 2 следует, что    (радиус
дуги CD вследствие малости dl равен
r, и угол FDC по этой же причине можно
считать прямым).

png» width=»264″>  Значит,
магнитная индукция поля прямого
тока   (5) 

32. Закон Био-Савара-Лапласа и применение
его к расчёту магнитного поля оси
кругового витка с током

Магнитное
поле в центре кругового проводника с
током (рис.
166). Как следует из рисунка, все элементы
кругового проводника с током создают
в центре магнитные поля одинакового
направления — вдоль нормали от витка.

Поэтому сложение векторов dB можно
заменить сложением их модулей.

Так как
все элементы проводника перпендикулярны
радиусу-вектору (sin =1)
и расстояние всех элементов проводника
до центра кругового тока одинаково и
равно R, то,
согласно (110.2),

Тогда

Следовательно,
магнитная индукция поля в центре
кругового проводника с током

Каждый
проводник с током создает в окружающем
пространстве магнитное поле. Электрический
же ток представляет собой упорядоченное
движение электрических зарядов. Поэтому
можно сказать, что любой движущийся в
вакууме или среде заряд создает вокруг
себя магнитное поле.

В результате
обобщения опытных данных был установлен
закон, определяющий поле В точечного
заряда Q, свободно
движущегося с нерелятивистской
скоростью v. Под
свободным движением заряда понимается
его движение с постоянной скоростью.

Этот закон выражается формулой

где r —
радиус-вектор, проведенный от заряда Q к
точке наблюдения М (рис.
168). Согласно выражению (113.1), вектор В направлен
перпендикулярно плоскости, в кото­рой
расположены векторы v и r,
а именно: его направление совпадает с
направлением поступательного движения
правого винта при его вращении от v к r.

Модуль
магнитной индукции (113.1) вычисляется по
формуле

где  —
угол между векторами v и r.

Сравнивая
выражения (110.1) и (113.1), видим, что движущийся
заряд по своим магнитным свойствам
эквивалентен элементу тока:

Приведенные
закономерности (113.1) и (113.2) справедливы
лишь при малых скоростях (v

Источник: https://studfile.net/preview/5443441/page:6/

Квантовый эффект Холла и его применение при построении эталона сопротивления

Квантовый эффект Холла, как и эффект Джозефсона, связан с использованием явления сверхпроводимости.

Если структуру металл — окисел — полупроводник (МОП-структура) охладить до температуры 4,2 К и поместить в сильное магнитное поле с индикацией 6…

где h — постоянная Планка, Дж с; е — заряд электрона, Кл. Размерность холловского сопротивления составит:

• Это есть размерность электрического сопротивления.
• Константа К. Клитдинга (величина холловского сопротивления) — гх = 25 812,807 Ом с погрешностью измерений, выполненных за рубежом и в нашей стране, не менее
• 1(Г8. По зарубежным данным, значение соотношения

в ближайшее годы будет подтверждено с погрешностью до 1(Г20. В этом случае существенно (как минимум на порядок) уменьшить погрешность измерения единицы электрического сопротивления г.

В настоящее время на экспериментальной установке ВНИИМим. Д. И. Менделеева получены результаты по поддержанию размера единицы электрического сопротивления с помощью квантового эффекта Холла со средним квадратическим отклонением менее 108.

Разумеется, погрешность воспроизведения единицы электрического сопротивления с помощью квантового эффекта Холла в ближайшие годы будет существенно уменьшаться.

Соответствующая установка, воспроизводящая размер Ома, включена в состав государственного эталона электрического сопротивления.

Другой составной частью эталона является группа из 10 манганиновых катушек сопротивления с номинальным значением 1 Ом, обеспечивающая воспроизведение Ома со средним квадратическим отклонением результата измерений ЗЮ~8 (по десяти независимым измерениям). Неис- ключенная составляющая систематической погрешности не превышает 3 10~7.

На основании рассмотренных квантованных напряжения и сопротивления можно представить квантовый эталон силы электрического тока ампер. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна

1. где dl — вектор, по модулю равный и совпадающий по направлению с током; В— вектор магнитной индукции.
2. Направление вектора dF можно найти по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
3. Из закона Ома получаем:

Учитывая, что U = Е1,

Заменяя I в формуле (1.2), получим:

где dF — сила Ампера; Ё — вектор напряженности электрического поля. Этот вектор направлен вдоль проводника и является величиной, имеющей физический смысл; В— вектор магнитной индукции внешнего магнитного поля, в которое помещен проводник с током (это также величина, имеющая физический смысл); R — электрическое сопротивление проводника.

Формула (1.4) выражает закон Ампера для участка цепи — потребителя тока, приведенный к корректному физическому виду в рамках классической электродинамики. Закон Ампера для участка цепи — источника тока подчиняется выражению (1.4).

Для полной цепи электрического тока:

Знак (-) перед правой частью уравнения (1.5) означает изменение потока энергии при переходе проводника на участок цепи — источник тока.

Таким образом, даже в рамках классической электродинамики можно вывести формулы для определения силы Ампера для цепи — потребителя тока, цепи — источника тока и полной цепи.

При реализации единицы 1 А (путем измерения силы) пользуются двумя установками.

Во-первых, измеряют силу, действующую на малую катушку в однородном магнитном поле, и, во- вторых, измеряют момент силы, действующий на малую катушку с током.

Рис. 1.12

Схема установки для «взвешивания» тока Дрисколла и Кутовско- го:

1 — электрический вывод из большой катушки; 2 — электровывод; 3 — электроподвод; 4 — коромысло аналитических весов.

Внутри большой фиксированной катушки с отводом от среднего витка обмотки (рис. 1.

12) длиной 27,5 см и диаметром 46 см (установка Национального бюро стандартов США) или длиной 50 см и диаметром 27,5 см (установка Немецкого бюро по контролю за материалами и товарами) помещается «измерительная катушка», на которую действует подлежащая измерению сила.

Электрическая цепь системы собрана таким образом, что подводимый к отводу от среднего витка большой катушки ток делится на две равные части и в противоположных направлениях протекает через верхнюю и нижнюю половины катушки.

При этом часть тока, обозначенная 12, проходит и через измерительную катушку. В половинах большой катушки 1 и 2 возникают (Н0 и Щ, рисунок 1.13) противоположно направленные магнитные поля.

В плоскости симметрии (при 2 = 0) вертикальная составляющая поля отсутствует. Поведение вертикальной составляющей поля вдоль оси 2 имеет тогда вид графика на рисунке 1.14. При 2 = 0 градиент напряженности отличен от нуля.

Так как

Рис. 1.13

Схема обмоток и полей

Рис. 1.14

Поведение вертикальной компоненты Нг магнитного поля

у измерительной катушки, если в ней течет ток 12, имеется магнитный момент М, то возникает вертикально направленная сила , действующая на эту катушку и измеряемая весами.

Сила между обмотками 2 а 3 действует в том же направлении, т. е. абсолютные значения обеих сил складываются. Следует сложить друг с другом силы, действующие между каждой парой соответствующих витков.

При определенном токе I аналитические весы уравновешиваются с помощью разновесов.

Затем меняют направление тока и одновременно увеличивают (или уменьшают) уравновешивающий груз, следя при этом за тем, чтобы снимаемый или добавляемый разновес был близок по своему весу к изменению величины силы. Показания стрелки весов дают остальные дробные части изменения силы.

Источник: https://ozlib.com/805684/tovarovedenie/kvantovyy_effekt_holla_primenenie_postroenii_etalona_soprotivleniya

Квантовый эффект Холла — Quantum Hall effect

Квантовый эффект Холла (или целое число , квантовый эффект Холла ) представляет собой квантово-механического версия эффекта Холла , наблюдается в двумерных электронных системах , подвергнутых низких температурах и сильных магнитных полей , в которых зал проводимости σ претерпевает квантового эффекта Холла переходов принимать на квантованных значений

σ знак равно я канал В зал знак равно ν е 2 час , { Displaystyle сигма = { гидроразрыва {I _ { текст {канал}}} {V _ { текст {Hall}}}} = Nu { гидроразрыва {е ^ {2}} {ч}}}

где I канал является каналом тока , V Hall является напряжение Холла , е является элементарный заряд и ч является постоянная Планка . Префактор ν известен как фактор заполнения, и может принимать либо целое число ( v , = 1, 2, 3, …

) или дробное ( ν = 1 / 3 , 2 / 5 , 3 / 7 , 2 / 3 , 3 / 5 , 1 / 5 , 2 / 9 , 3 / 13 , 5 / 2 , 12 / 5 , … ) значения.

Квантовый эффект Холла упоминаются как целое или дробный квантовый эффект Холла в зависимости от того , ν представляет собой целое или дробное число , соответственно.

Поразительная особенность целочисленного квантового эффекта Холла является сохранение квантования (то есть плато Холла), а плотность электронов изменяется.

Дробный квантовый эффект Холла является более сложным, так как ее существование зависит главным образом от электрон-электронных взаимодействий. Дробный квантовый эффект Холла также следует понимать как целочисленный квантовый эффект Холла, хотя и не электроны , но шихтовый поток композитов , известных как композитные фермионы .

В 1988 году было предложено , что существует квантовый эффект Холла без уровней Ландау . Этот квантовый эффект Холла называют квантовый эффект Холла аномального (QAH). Существует также новая концепция эффекта Холла квантовый спин , который является аналогом квантового эффекта Холла, где спиновые токи текут вместо заряда токов.

Приложения

Квантование проводимости Холла имеет важное свойство быть чрезвычайно точным. Фактические измерения проводимости Холла было установлено, целые или дробные кратные е 2 / ч почти одна часть в миллиард.

Это явление, называемое точное квантование , было показано, что тонкое проявление принципа калибровочной инвариантности .

Это позволило для определения нового практического стандарта для электрического сопротивления , на основе сопротивления кванта , заданной Клитцинг постоянной R K = ч / е 2 = 7004258128075570000 ♠25 812 0,807 557 (18)  Ом .

Это был назван в честь Клаус фон Клитцингу , открывателя точного квантования.С 1990 года фиксированное обычное значение R К-90 была использована в калибровок сопротивления по всему миру.

С 16 ноября 2018 года, обычное значение было отменено в связи с решением , чтобы исправить значения часов (постоянная Планка) и е (элементарный заряд) на 26 — м заседании Генеральной конференции по мерам и весам. Квантовый эффект Холла также обеспечивает чрезвычайно точное независимое определение постоянная тонкой структуры , количество фундаментального значения в квантовой электродинамике .

история

Целочисленное квантование проводимости Холла первоначально было предсказано Андо, Мацумото и Uemura в 1975 году, на основе приближенного вычисления , которые они сами не верили , чтобы быть правдой.

Некоторые исследователи впоследствии наблюдали эффект в опытах , проведенных на инверсионном слое МОП — транзисторов .

И только в 1980 году , что Клаус фон Клитцинг , работающий на высокой лаборатории магнитного поля в Гренобле с образцами на основе кремния , разработанного Майкл Pepper и Gerhard Дорд, сделал неожиданное открытие , что проводимость Холла была точно квантуется.

Эксперименты Большинство целочисленный квантовый эффект Холла теперь выполняются на арсенида галлия гетероструктурах , хотя многие другие полупроводниковые материалы могут быть использованы. В 2007 году число квантовый эффект Холла был зарегистрирован в графене при температурах до комнатной температуры, и в магния цинка оксида ZnO-Mg х Zn 1- х O.

Эффект Integer квантовый эффект Холла — уровни Ландау

В двух измерениях, когда классические электроны подвергаются воздействию магнитного поля они следуют круговым орбитам циклотрона. Когда система рассматривается квантовомеханически, эти орбиты квантуются. Уровни энергии этих квантованных орбиталей принимают дискретные значения:

Е N знак равно ℏ ω с ( N + 1 2 ) , { Displaystyle Е- {п} = HBAR омега _ { текст {с}} влево (п + { tfrac {1} {2}} справа),}

где ω с = еВ / м частота циклотронного.

Эти орбитали известны как уровни Ландау , и в слабых магнитных полях, их существование приводит к появлению множества «квантовых колебаний» , таких как осцилляции Шубникова-де — Гааза и эффект де Гааза-ван Альфена (который часто используется для отображения поверхности Ферми металлов).

Для сильных магнитных полей, каждый уровень Ландау сильно вырожденный (т.е. существует множество состояний одиночных частиц , которые имеют одинаковую энергию E п ). В частности, для образца области A , в магнитном поле В , вырождение каждого уровня Ландау

N знак равно г s В A φ 0 , { Displaystyle N = г _ { текст {s}} { гидроразрыва {BA} { Phi _ {0}}}}

где г ы представляет собой фактор 2 для спинового вырождения, и ф 0 ≈ 6985200000000000000 ♠2 × 10 -15  Вб является квант магнитного потока . При достаточно сильных магнитных полей, каждый уровень Ландау может иметь столько состояний , что все свободные электроны в системе сидят лишь несколько уровней Ландау; именно в этом режиме , когда один наблюдает квантовый эффект Холла.

Математика

Целые , которые появляются в эффекте Холла являются примерами топологических квантовых чисел . Они известны в математике как первые Черна чисел и тесно связаны с фазой Берри . Яркая модель представляет большой интерес в этом контексте является моделью Азбели-Харпер-Хофштадтер которого квантового фазовой диаграмма представляет собой бабочки Хофштадтер показан на рисунке. Вертикальная ось сила магнитного поля , а горизонтальная ось представляет собой химический потенциал , который фиксирует плотность электронов. Цвета представляют проводимости целого Hall. Теплые цвета представляют собой целые положительные числа и холодные цвета отрицательные целые числа. Однако следует отметить, что плотность состояний в этих областях квантуется Холла проводимости равна нулю; следовательно, они не могут производить плато наблюдается в экспериментах. Фазовая диаграмма фрактальна и имеет структуру на всех уровнях. На рисунке есть очевидное самоподобие . При наличии расстройства, которое является источником плато видели в экспериментах, эта диаграмма сильно отличается и фрактальная структура в основном вымывается.

Что касается физических механизмов, примесей и / или конкретных состояний (например, краевые токи) имеют важное значение для обоих «целое» и «» дробных эффектов.

Кроме того, кулоновское взаимодействие также имеет важное значение в дробном квантовом эффекте Холла .

Наблюдается сильное сходство между целочисленного и дробного квантовых эффектов Холла объясняется тенденцией электронов с образованием связанных состояний с четным числом квантов магнитного потока, называемых композитных фермионов .

Интерпретация атома Бора константы фон Клитцинг

Значение константы фона Клитцинга может быть получено уже на уровне одного атома в рамках модели Боры , глядя на него в качестве одноэлектронного эффекта Холла.

В то время как во время циклотронного движения по круговой орбите, центробежная сила уравновешивается силой Лоренца , ответственной за поперечное наведенное напряжение и эффект Холла можно посмотреть на разности потенциалов Кулона в атоме Бора в качестве индуцированного одного напряжения атома Холла и периодического движение электрона по окружности ток Холла. Определение одного атома тока Холла как скорость один заряд электрона делает Kepler обороты с угловой частотой е { Displaystyle е}
ω { Displaystyle Omega}

я знак равно ω е 2 π , { Displaystyle I = { гидроразрыва { омега е} {2 пи}}}

и индуцированное напряжение Холла как разность между ядром водорода кулоновским потенциалом в электронной орбитальной точке и на бесконечности:

U знак равно В С ( ∞ ) — В С ( р ) знак равно 0 — В С ( р ) знак равно е 4 π ε 0 р { Displaystyle U = V _ { текст {C}} ( infty) -V _ { текст {C}} (г) = 0-V _ { текст {C}} (г) = { гидроразрыва {е} {4 р эпсилон _ {0} г}}}

р Бор ( N ) знак равно U я знак равно N час е 2 { Displaystyle R _ { {текст}} Бор (п) = { гидроразрыва {U} {Я}} = {п гидроразрыва {ч} {е ^ {2}}}}

который для атома Бора является линейным , но не в обратную целого числа п .

Релятивистские аналоги

Релятивистские примеры целочисленного квантового эффекта Холла и квантового спинового эффекта Холла возникает в контексте решеточной калибровочной теории .

Смотрите также

Рекомендации

дальнейшее чтение

• ДР Yennie (1987). «Интегральный квантовый эффект Холла для неспециалистов». Rev. Mod. Phys . 59 (3): 781-824. Bibcode : 1987RvMP … 59..781Y . DOI : 10,1103 / RevModPhys.59.781 .
• Д. Се; Д. Цянь; Л. Врэй; Ю. Ся; YS Hor; RJ Cava; MZ Hasan (2008). «Топологическая Дирака изолятор в квантовой фазе спинового Холла». Природа . 452 (7190): 970-974. Arxiv : 0902,1356 . Bibcode : 2008Natur.452..970H . DOI : 10.1038 / nature06843 . PMID  18432240 .
• 25 лет квантового эффекта Холла , К. фон Клитцинга, Пуанкаре семинар (Париж-2004). Постскриптум . Pdf .
• Magnet Lab Пресс — релиз квантовый эффект Холла Наблюдаемые при комнатной температуре
• Avron, Джозеф E .; Осадчий, Даниил; Seiler, Ruedi (2003). «Топологические Посмотри квантовый эффект Холла». Physics Today . 56 (8): 38. Bibcode : 2003PhT …. 56h..38A . DOI : 10,1063 / 1,1611351 .
• Zyun Ф. Ezawa: Квантовый эффект Холла — поле Теоретический подход и смежные темы. World Scientific, Сингапур 2008, ISBN  978-981-270-032-2
• Sankar Д. Шарма, Aron Pinczuk: Перспективы в Квантовый эффект Холла. Wiley-VCH, Weinheim 2004, ISBN  978-0-471-11216-7
• А. Баумгартнер; Т. Ihn; К. Энсслин; К. Maranowski; А. Госсард (2007). «Переходный Квантовый эффект Холла в экспериментах сканирования затвора». Phys. Rev. B . 76 (8): 085316. Bibcode : 2007PhRvB..76h5316B . DOI : 10,1103 / PhysRevB.76.085316 .
• EI Рашбы и В. Б. Тимофеев, квантовый эффект Холла, Совы. Phys. -. Полупроводники v 20, стр 617-647 (1986)..

Источник: https://ru.qwe.wiki/wiki/Quantum_Hall_Effect