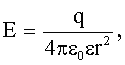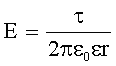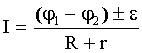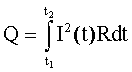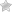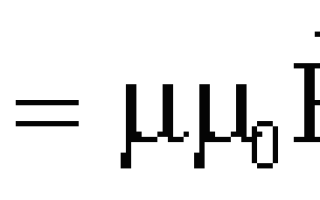Формула нахождения потенциальной разницы между точками в электромагнитном поле

Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

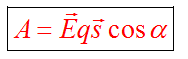
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.

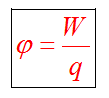
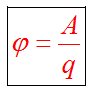
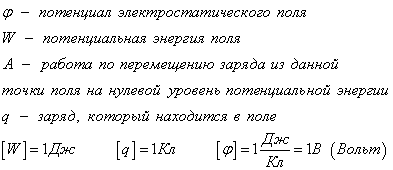
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.

Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

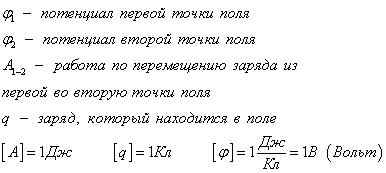
Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

• Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
• Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
• От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Как определить знак потенциала

При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.

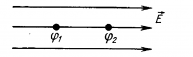
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.

Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.

Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.

Зависимость напряженности и потенциала от расстояния

Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен

Напряжение в природе

Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В. Напряжение в телефонных сетях может достигать 60 В.

Электрический угорь способен создавать напряжение до 650 В.

Энергия взаимодействия зарядов*

1. Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
2. Аналогично Тогда энергия взаимодействия двух точечных зарядов
3. Энергия взаимодействия n зарядов

Источник: https://fizmat.by/kursy/jelektrichestvo/potencial

Определение напряженности электрического поля с помощью потенциала

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Формулу 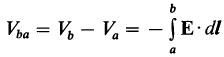можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е. Посмотрим, как это делается.

• Уравнение можно переписать в дифференциальной форме:
• dV = -E·dl = -Eldl,
• где dV — бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а El — составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.Тогда:

Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl.

Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:

Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z, то уравнение (24.8) можно записать в виде:

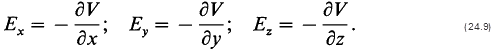
Здесь dV/dx — частная производная V по направлению х при условии, что у и z фиксированы.

В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее.

Вообще говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.

9) — напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем векторы.

Электростатическая потенциальная энергия

Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы в которых, обусловленные другими зарядами, равны соответственно Va и Vb. Изменение электростатической потенциальной энергии заряда q в поле других зарядов составляет:

ΔU = Ub — Ua = q(Vb — Va) = qVba

Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы? Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга.

Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила.

Если к нему поднести второй точечный заряд, Q2, потенциал в точке, где находится второй заряд, будет равен:

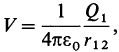
Здесь r1 2 — расстояние между зарядами. Потенциальная энергия двух зарядов равна:

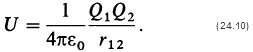
Она характеризует работу, необходимую для перемещения заряда Q2 из бесконечности (V = 0) на расстояние r1 2 до заряда Qi (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).

Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения.

Работа по сближению зарядов Q2 и Q1 определяется выражением (24.

10); чтобы перенести заряд Q3 из бесконечности в точку на расстоянии r1 3 от Q1 и на расстоянии r2 3 от Q2, требуется совершить работу:

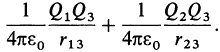
В этом случае потенциальная энергия системы трех точечных зарядов будет равна:

Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды). Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее.

Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q1 и -Q1 первого диполя и Q2 и -Q2 второго диполя.

Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния.

В этом случае нас не интересует взаимная потенциальная энергия зарядов Q1 и -Q1 или Q2 и -Q2; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q1 и Q2 ; Q1 и -Q2 ; -Q1 и Q2 ; -Q1 и -Q2.

Заключение

Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками.

Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение потенциальной энергии заряда q при прохождении им разности потенциалов Vbа равно ΔU = qVba.

Разность потенциалов Vbа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d — расстояние вдоль силовой линии поля между этими точками. В неоднородном электрическом поле Е соответствующее выражение имеет вид 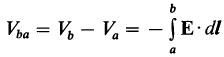. Таким образом, зная Е, всегда можно определить Vbа. Если значение V известно, то составляющие напряженности поля Е можно найти, обращая приведенное соотношение:

Еx = -dV/dх , Еy = -dV/dу , Ez = -dV/dz .

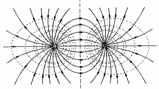
Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:

1. Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.
2. где r — расстояние от элемента заряда dq до точки, в которой определяется V.
3. Продолжение следует. Коротко о следующей публикации:
4. Электрическая емкость, диэлектрики, накопление электрической энергии.

Конденсатор — устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.

• Альтернативные статьи: Постоянный ток, Переменный ток.
• Замечания и предложения принимаются и приветствуются!

Источник: https://tel-spb.ru/statika/pole-potencial.php

Потенциал. Разность потенциалов. Напряжение.Эквипотенциальные поверхности

Потенциал. Разность потенциалов. Напряжение.
Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
— следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.          Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов    Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Связь между напряженностью и напряжением.
Из доказанного выше:   →      напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
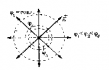
Из этого соотношения видно: Вектор напряженности направлен в сторону уменьшения потенциала. Электрическое поле существует, если существует разность потенциалов. Единица напряженности:     —   Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке.
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.
Потенциальная энергия взаимодействия зарядов.
Потенциал поля точечного заряда
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.

Источник: https://www.eduspb.com/node/1761

Магнитное поле – FIZI4KA

ЕГЭ 2018 по физике ›

Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов.

Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы.

Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током).

Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются.

Свойства магнитного поля:

• магнитное поле материально;
• источник и индикатор поля – электрический ток;
• магнитное поле является вихревым – его силовые линии (линии магнитной индукции) замкнутые;
• величина поля убывает с расстоянием от источника поля.

Важно! Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю.

• Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока.
• Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы.
• Силовая характеристика магнитного поля – вектор магнитной индукции ​( vec{B} )​. Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике ​( I )​ и его длине ​( l )​:

1. Обозначение – ( vec{B} ), единица измерения в СИ – тесла (Тл).
2. 1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н.
3. Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле.
4. Направление вектора магнитной индукции можно определить по правилу буравчика:
5. если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.
6. Для определения магнитной индукции нескольких полей используется принцип суперпозиции:
7. магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности:

Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным.

Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней.

Свойства магнитных линий:

• магнитные линии непрерывны;
• магнитные линии замкнуты (т.е. в природе не существует магнитных зарядов, аналогичных электрическим зарядам);
• магнитные линии имеют направление, связанное с направлением тока.

Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле.

На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил ​( M )​:

где ​( I )​ – сила тока в проводнике, ​( S )​ – площадь поверхности, охватываемая контуром, ​( B )​ – модуль вектора магнитной индукции, ​( alpha )​ – угол между перпендикуляром к плоскости контура и вектором магнитной индукции.

Тогда для модуля вектора магнитной индукции можно записать формулу:

где максимальный момент сил соответствует углу ​( alpha )​ = 90°.

В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции.

Взаимодействие магнитов

Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле.

Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный ​( N )​ и южный ​( S )​.

Важно! Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс.

Разделить полюса магнита нельзя.

Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи.

Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств.

Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются.

Магнитное поле проводника с током

Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.

• Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.
• Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.
• Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.

При изменении направления тока линии магнитного поля также изменяют свое направление.

По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.

Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.

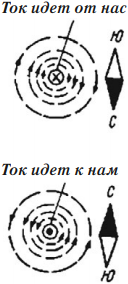
Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.

В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление.

Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются.

При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.

Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.

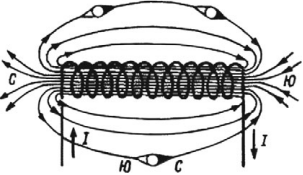
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.

1. Направление линий магнитной индукции катушки с током находят по правилу правой руки:
2. если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.
3. Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:
4. если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.

Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.

Сила Ампера

Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле.

Закон Ампера: на проводник c током силой ​( I )​ длиной ​( l )​, помещенный в магнитное поле с индукцией ​( vec{B} )​, действует сила, модуль которой равен:

где ​( alpha )​ – угол между проводником с током и вектором магнитной индукции ​( vec{B} )​.

Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​( B_perp )​ входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.

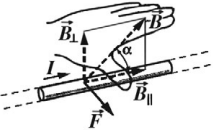
Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции.

Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток.

Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера.

В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр).

Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода.

• Коэффициент полезного действия электродвигателя:
• где ​( N )​ – механическая мощность, развиваемая двигателем.
• Коэффициент полезного действия электродвигателя очень высок.
• Алгоритм решения задач о действии магнитного поля на проводники с током:

• сделать схематический чертеж, на котором указать проводник или контур с током и направление силовых линий поля;
• отметить углы между направлением поля и отдельными элементами контура;
• используя правило левой руки, определить направление силы Ампера, действующей на проводник с током или на каждый элемент контура, и показать эти силы на чертеже;
• указать все остальные силы, действующие на проводник или контур;
• записать формулы для остальных сил, упоминаемых в задаче. Выразить силы через величины, от которых они зависят. Если проводник находится в равновесии, то необходимо записать условие его равновесия (равенство нулю суммы сил и моментов сил);
• записать второй закон Ньютона в векторном виде и в проекциях;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

Сила Лоренца

1. Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

2. Формула для нахождения силы Лоренца:
3. где ​( q )​ – заряд частицы, ​( v )​ – скорость частицы, ​( B )​ – модуль вектора магнитной индукции, ​( alpha )​ – угол между вектором скорости частицы и вектором магнитной индукции.

4. Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​( B_perp )​ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.
5. Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно! Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно.

• В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.
• Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:
• где ​( m )​ – масса частицы, ​( v )​ – скорость частицы, ​( B )​ – модуль вектора магнитной индукции, ​( q )​ – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

1. Угловая скорость движения заряженной частицы:

Важно! Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы.

Если вектор скорости направлен под углом ​( alpha )​ (0° < ( alpha ) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.

В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, ​( vec{v}_2 )​, параллелен вектору ( vec{B} ), а другой, ( vec{v}_1 ), – перпендикулярен ему.

Вектор ( vec{v}_1 ) не меняется ни по модулю, ни по направлению. Вектор ( vec{v}_2 ) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости ( vec{v}_1 ). Частица будет двигаться по окружности.

Период обращения частицы по окружности – ​( T )​.

Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору ( vec{B} ). Частица движется по винтовой линии с шагом ​( h=v_2T )​.

• Важно! Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:
• Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».
• Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

• сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
• изобразить силы, действующие на заряженную частицу;
• определить вид траектории частицы;
• разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
• составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
• выразить силы через величины, от которых они зависят;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

Основные формулы раздела «Магнитное поле»

Источник: https://fizi4ka.ru/egje-2018-po-fizike/magnitnoe-pole.html

Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме.

Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона.

Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип

Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.

Смотрите также основные формулы оптики

Таблица основных формул электричества и магнетизма

Физические законы, формулы, переменные	Формулы электричество и магнетизм
Закон Кулона: где q1 и q2 — величины точечных зарядов, ԑ1  — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1),r — расстояние между зарядами.
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля.
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями	1) 2) 3) 4)
Потенциал электрического поля: где W — потенциальная энергия заряда q0 .
Потенциал поля точечного заряда на расстоянии r от заряда:
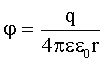
По принципу суперпозиции полей, напряженность:
Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 :
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля:	1)  2)
Электроемкость уединенного проводника:
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение.
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами.
Энергия заряженного конденсатора:
Сила тока:
Плотность тока: где S — площадь поперечного сечения проводника.
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения.
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС:    где ε — ЭДС источника тока,    R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи:	1) 2)  3)  4)
Закон Джоуля-Ленца  1) для однородного участка цепи постоянного тока:    где Q — количество тепла, выделяющееся в проводнике с током,    t — время прохождения тока;  2) для участка цепи с изменяющимся со временем током:	1) 2)
Мощность тока:
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1),µ0 — магнитная постоянная,H — напряженность магнитного поля.
Магнитная индукция (индукция магнитного поля):  1) в центре кругового тока     где R — радиус кругового тока,  2) поля бесконечно длинного прямого тока      где r — кратчайшее расстояние до оси проводника;  3) поля, созданного отрезком проводника с током    где ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля;  4) поля бесконечно длинного соленоида     где n — число витков на единицу длины соленоида.	1) 2)  3)  4)
Сила Лоренца: по модулю где F — сила, действующая на заряд, движущийся в магнитном поле,v — скорость заряда q,α — угол между векторами v и B.
Поток вектора магнитной индукции (магнитный поток через площадку S):  1) для однородного магнитного поля ,    где α — угол между вектором B и нормалью к площадке, 2) для неоднородного поля	1) 2)
Потокосцепление (полный поток): где N — число витков катушки.
Закон Фарадея-Ленца: гдеԑi — ЭДС индукции.
ЭДС самоиндукции: где L — индуктивность контура.
Индуктивность соленоида: где n — число витков на единицу длины соленоида, V — объем соленоида.
Энергия магнитного поля:
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура.
Работа по перемещению замкнутого контура с током I в магнитном поле:

Источник: https://infotables.ru/fizika/95-osnovnye-formuly-po-fizike-elektrichestvo-i-magnetizm

Магнитное поле. Основные теоретические положения, страница 6

Магнитное   напряжение   между   произвольными   точками   Е   и   G: UmЕG =.

В областях, не занятых проводниками, магнитное поле является потенциальным, следовательно, магнитное напряжение не зависит от путей интегрирования, если они не образуют контуров, связанных с токами.

Поэтому нужно выбрать путь интегрирования ЕG таким, чтобы вычисление интеграла было простым – вдоль радиальных линий и по окружности. Таким образом,

UmЕG = UmЕF + UmFG = -·b + 0 = -·b.

Выводы. 1. Точки, лежащие на радиальной к проводнику линии, имеют один и тот же потенциал, то есть радиальная линия является эквипотенциалью.

2. Магнитное напряжение зависит от угла между точками и не зависит от расстояния от них до провода. Напряжение для произвольной кривой  LN вычисляется по формуле

UmLN = ±·g;                                     (14.4)

здесь g – выраженный в радианах угол, под которым дуга LN видна из центра проводника.

3. Если интегрирование осуществляется вдоль силовых линий, магнитное напряжение положительно, если против – отрицательно.

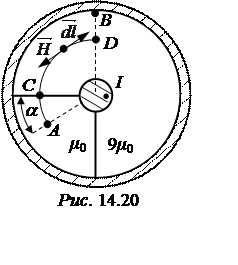
ЗАДАЧА 14.18. По жиле коаксиального кабе-ля (рис. 14.20) протекает ток   I= 360 А.  Определить магнитное напряжение между точками А и B, если   a= 30°.

Решение

Магнитное напряжение между точками А и В определим по формуле  UmAB =. путь движения выберем А—С—D—В (рис. 14.20), учитывая, что из-за различных магнитных проницаемостей сред напряженности в них разные. Тогда

• UmAB ==++= —Н1·lAC – Н2·lCD, где    = 0  из-за перпендикулярности векторов    и  ;
•   и   –  напряженности в областях с  m0  и  9m0,  соответственно;
• напряжения Н·l взяты с минусом, поскольку направления векторов        и   противоположные.
• Величины Н1 и Н2 определим с помощью закона полного тока
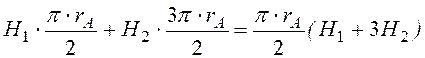• == I.
• В силу того, что нормальная составляющая вектора  на границе раздела двух сред непрерывна, имеем
• mН1 = 9mН2.
• Решая совместно два последних уравнения, получаем
• Н1 =;    Н2 =.
• Учитывая, что  lAC = rA·a,  где a должно быть выражено в радианах, и  lCD = rA·,  получаем
• UmAB = —Н1·lAC – Н2·lCD = -·rA·–·rA·== -120 A.

Задача 14.19. Уединённый провод с током   I = 10 А   находится  на границе раздела сред (рис. 14.21):  m1 = 2,   m2 = 4,   m3 = 6.   Координаты точек  хА = уА = 10 см,    хВ = -5 см,   уВ = -15 см.  Требуется:

1. 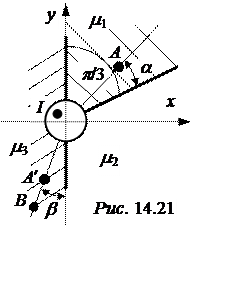 Рассчитать напряжённости магнитного поля в точках А и В, а также магнитное напряжение между ними.

2. Считая, что А и В являются точками сечения длинных сторон прямоугольной рамки длиной   l = 1 м  и с числом витков w = 100,  найти магнитный поток рамки и взаимную индуктивность провода и рамки.

1. Решение
2. Вычислим расстояния от центра провода до точек А и В:
3. rA = 10= 14,14 см,   rB == 15,81 см.
4. Для расчета напряжённости магнитного поля в точке А проведём через неё окружность с центром, совпадающим с осью провода. На основании закона полного тока можно записать:
5. H1·rA + H2·rA + H3·p·rA = I, где  H1,  H2,  H3 –  напряженность поля в среде с проницаемостью, соответ-ственно,  m1, m2, m3.

Границы расположены радиально, поэтому векторы  и  на границе имеют только нормальную составляющую. Граничное условие  В1n = В2n = В3n, откуда  m1·H1 = m2·H2 = m3·H3.

• Таким образом,    H1·(rA+·rA +·prA) = I,  откуда
• HА = H1 = I/(rA +·rA +·prA) =
• = 10·3/((1+0,5·2+1/3·3)·p·0,1414) = 22,51 А/м.
• Аналогично, напряжённость в точке В:
• HВ = H3 =H1 =I/(rВ+·rВ+·prВ) =
• = 10/((1+0,5·2+1/3·3)·p·0,1581) = 6,71 А/м.

магнитное напряжение между точками А и В при движении по часовой стрелке (против силовых линий) можно вычислить по формуле (см. зад. 14.18):     UmAB = —H1·rA·a – H2·rA·– H3·rA·b;

1. H1·rA = 30/(3p),    H2·rA = 15/(3p),   H3·rA = 10/(3p),
2. a = – arctg= – = рад,   b = arctg= arctg= 0,3218 рад.
3. Таким образом,    UmAB = -––·0,3218 = -5,24 А.

Источник: https://vunivere.ru/work61711/page6