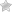О скважности импульсов сигнала: отношение периода следования к длительности импульса

Общая характеристика импульсного сигнала

Виды импульсных сигналов. Под импульсной техникой понимают область радиоэлектроники, изучающую формирование импульсных сигналов и их прохождение через электрические цепи. Импульсный сигнал может состоять из одного или серии импульсов.

Под импульсом понимают быстрое появление и исчезновение тока или напряжения, т. е. кратковременное действие тока или напряжения на электрическую цепь или устройство. В импульсной технике различают два вида импульсных сигналов — видеоимпульсы (рис.

1, а), представляющие собой кратковременные односторонние (относительно оси времени) изменения напряжения или тока в цепи постоянного тока, и радиоимпульсы (рис.

Форма импульсов

 Импульсы могут иметь прямоугольную, трапецеидальную, колоколообразную, треугольную и экспоненциальную

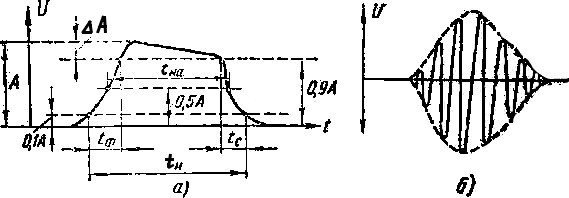Рис. 1. Одиночные импульсы: а — видеоимпульс, б — радиоимпульс

форму (рис. 2). В импульсе различной формы различают фронт, вершину и спад. Импульсы могут быть положительной или отрицательной полярности. Импульсы положительной полярности на графиках изображают выше горизонтальной оси времени, а отрицательной — ниже оси.

Параметры импульсов. Каждый импульс характеризуется амплитудой А (см. рис. 1, а), длительностью импульса tи, длительностями фронта tф, спада tс, снижением вершины ΔА, а также мощностью в импульсе Ри.

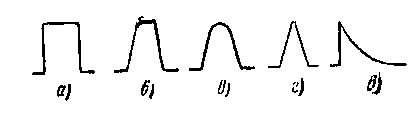Рис. 2. Формы импульсов: а — прямоугольная, б — трапецеидальная, в — колоколообразная, е — треугольная, д —экспоненциальная

Амплитуда однополярного импульса характеризуется величиной (размахом) напряжения или тока от нуля до максимального значения импульса данной формы. В двустороннем импульсе величина от вершины положительного до вершины отрицательного импульса называется полным размахом импульса (полной амплитудой Aп).

Длительность импульса tп — интервал времени, в течение которого ток или напряжение действует на электрическую цепь. В реальных схемах искажается форма импульсов, поэтому длительность определяют на уровне 0,1A и реже по основанию импульса. Активную длительность импульса tи.a измеряют на уровне 0,5 А.

Длительность фронта tф и спада tc оценивается интервалом времени, в течение которого амплитуда импульса нарастает от 0,1 до 0,9 своего максимального значения и падает от 0,9A до 0,1А. В большинстве случаев желательно иметь минимальные tф и to.

Снижение вершины ΔА практически не должно превышать (0,01—0,05) А.

Мощность в импульсе характеризуется отношением энергии W, выделенной в цепи при прохождении импульса, к его длительности tи:

Для периодической последовательности импульсов (рис, 3, а) свойственно следование импульсов через равные промежутки времени. Ее характеризуют следующие параметры.

Период следованияТи — интервал времени от момента появления одного импульса до момента появления следующего импульса той же полярности.

Частота следования Fи, являющаяся величиной, обратной периоду следования, т. е.

Длительность паузы Ти — время между моментом окончания одного импульса и началом другого:

Скважность импульсов Q, определяемая как отношение периода следования Ти к длительности tи

Среднее значение импульсного тока (напряжения) получается, если ток (напряжение) импульса равномерно распределить на весь период так, чтобы площадь прямоугольника IсрTи (рис. 3,б) была равновелика площади импульса Sи

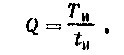
Коэффициент заполнения — величина, обратная скважности, показывающая, какую часть периода занимает импульс:

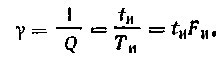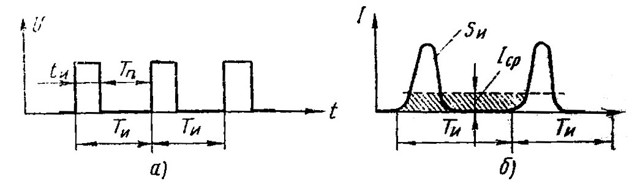Рис. 3. Периодическая последовательность импульсов: а — прямоугольных, б — колоколообразных

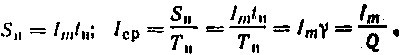
• Средняя мощность PСр определяется отношением энергии W, выделенной в цепи за период следования импульса Tи, к длительности этого периода:
• Очевидно, РсрТи=Pиtи, откуда
• Электронные приборы для импульсных схем очень часто выбирают по средней мощности.
• Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.

Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.

С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени.

То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени.

Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.

· Однополярные сигналы — это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.

· Двухполярные сигналы — эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.

Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:

· Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.

· Частота — это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, ( ). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.

· Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.

Периодические сигналы

Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.

Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.

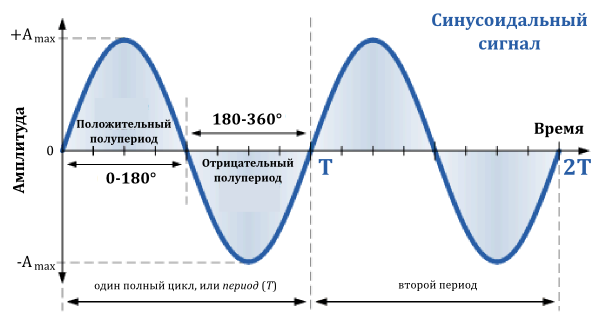
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.

1. Синусоидальный сигнал
2. Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
3. Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то (T = ).

Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.

• Соотношения между периодом сигнала и его частотой:
• Гц
• c
• Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц

Префикс	Определение	Запись	Период
Кило	тысяча	кГц	1 мс
Мега	миллион	МГц	1 мкс
Гига	миллиард	ГГц	1 нс
Тера	триллион	ТГц	1 пс

Меандр

Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.

Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.

1. Для меандра, время заполнения равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
2. Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
3. Гц
4. Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «» маленькими значениями амплитуды.

Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.

Прямоугольный сигнал

Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.

В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.

На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.

• Отношение периода повторения сигнала , к длительности положительного импульса , называют скважностью:
• Величину обратную скважности называют коэффициентом заполнения (duty cycle):
• Пример расчета

Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.

Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).

Гц

Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала.

Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку.

Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».

Треугольные сигналы

Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.

В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.

Пилообразный сигнал

Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.

Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным.

Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник.

Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.

Импульсы и запускающие сигналы (триггеры)

Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.

Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения.

Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.

1. Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
2.  Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например:
3. · Амплитудно-модулированный сигнал
4. · Частотно-модулированный сигнал
5. · Фазо-модулированный сигнал
6. · Фазо-частотно-модулированный сигнал
7. · Фазо-кодо-манипулированный сигнал

Источник: https://megaobuchalka.ru/14/40126.html

Формы и характеристики электрических сигналов | РОБОТОША

Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.

Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.

С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени.

 То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени.

Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.

• Однополярные сигналы — это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.
• Двухполярные сигналы — эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.

Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:

• Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.
• Частота — это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, (). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
• Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.

Периодические сигналы

Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.

Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.

Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.

Синусоидальный сигнал

• 
• Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
• Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то (T = ).

Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.

1. Соотношения между периодом сигнала и его частотой:
2. Гц
3. c
4. Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц

Префикс	Определение	Запись	Период
Кило	тысяча	кГц	1 мс
Мега	миллион	МГц	1 мкс
Гига	миллиард	ГГц	1 нс
Тера	триллион	ТГц	1 пс

Меандр

Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.

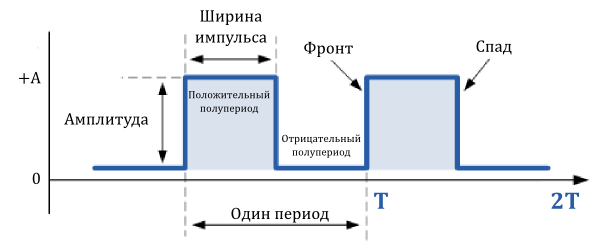
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.

• Для меандра, время заполнения равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
• Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
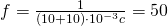• Гц
• Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.

Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае,  или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.

Прямоугольный сигнал

Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.

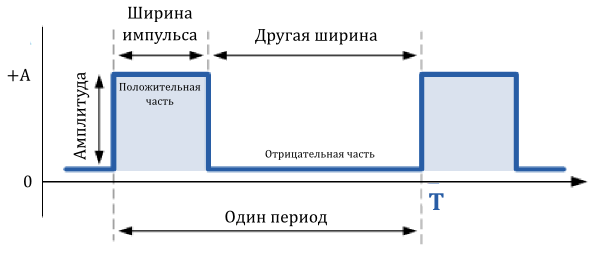
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.

На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.

1. Отношение периода повторения сигнала , к длительности положительного импульса , называют скважностью:
2. Величину обратную скважности называют коэффициентом заполнения (duty cycle):

Пример расчета

Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.

Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).

Гц

Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала.

Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в  нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку.

 Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».

Треугольные сигналы

Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями.

Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой.

 Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.

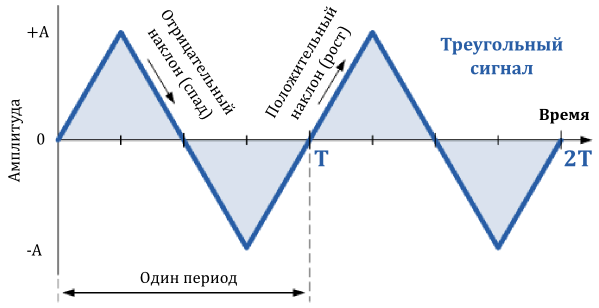
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.

В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.

Пилообразный сигнал

Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.

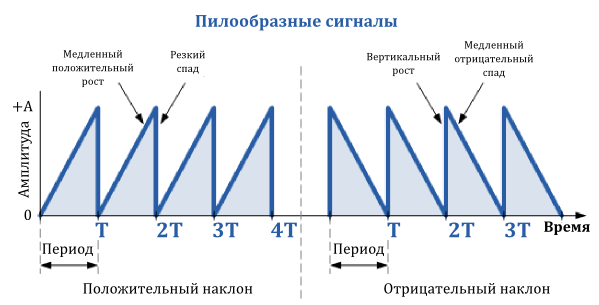
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным.

Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник.

Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.

Импульсы и запускающие сигналы (триггеры)

Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.

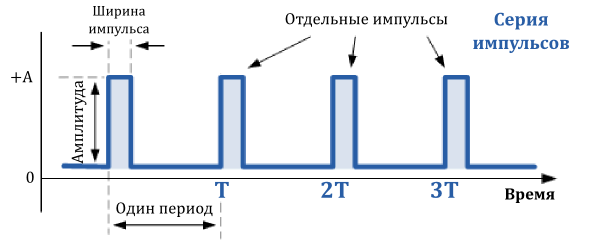
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал.

Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения.

Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.

• 
• Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
• Я рассмотрел здесь только основные виды электрических сигналов. Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например: 

• Амплитудно-модулированный сигнал
• Частотно-модулированный сигнал
• Фазо-модулированный сигнал
• Фазо-частотно-модулированный сигнал
• Фазо-кодо-манипулированный сигнал

Подробно я вернусь к ним в своих последующих публикациях.

Источник: https://robotosha.ru/electronics/electrical-waveforms.html

Широтно-Импульсная Модуляция (Pulse-Width Modulation)

   Уже в первых экспериментах с коллекторным моторчиком и батарейкой можно было заметить, что при частом попеременном включении и выключении электромотора частота вращения его ротора изменяется.

То есть происходила регулировка скорости вращения путём периодичного включения и отключения тока через моторчик. Если изменять при этом время в подключённом состоянии и длину паузы между подключениями, можно регулировать скорость вращения мотора.

Такой же эффект проявляется практически с любым потребителем электрического тока, имеющим определённую инерцию, т.е. способным запасать энергию.

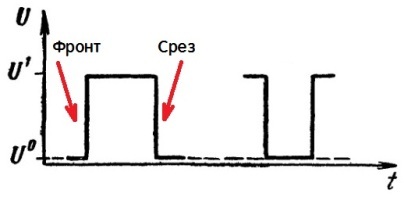
   В цифровой электронике все сигналы могут быть представлены всего двумя уровнями напряжения: «логической единицей» и «логическим нулём». Это всего лишь условные величины напряжения.

«Логической единице» приписывается высокий уровень напряжения, обычно около 2-3 вольт, «логическим нулём» считается близкое к нулю напряжение.

Цифровые импульсы графически изображаются прямоугольными или трапециевидными по форме:

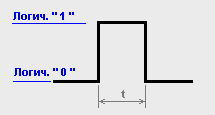
   Главной величиной одиночного импульса является его длина. Длина импульса — это отрезок времени, в течение которого рассматриваемый логический уровень имеет одно устойчивое состояние.

На рисунке латинской буквой t отмечена длина импульса высокого уровня, то есть логической «1».

Длина импульса измеряется в секундах, но чаще в миллисекундах (мс /  ms), микросекундах (мкс / μs) и даже наносекундах (нс / ns).

   Чем больше импульсов, тем больше информации можно ими передать. У множества импульсов появляется много характеристик.

• 
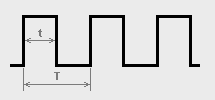
•    Частота импульсов F — это количество полных импульсов за 1 с, Гц / Hz.
•    Период импульсов T — это промежуток времени, между двумя характерными точками двух соседних импульсов, обычно между двух фронтов или двух спадов соседних импульсов. 
• T=1/F
• Если длина импульса t точно равна половине периода T, то такой сигнал часто называют «меандр». 
•    Скважность импульсов S — отношение периода импульсов к их длительности:
• S=T/t
•    Скважность безразмерная величина и может быть выражена в процентах.
•    Коэффициент заполнения / Duty cycle D — величина, обратная скважности обычно выражается в процентах:
• D=1/S
•    Если увеличивать или уменьшать длину импульса и при этом на столько же уменьшать или увеличивать паузу между импульсами, то период следования импульсов и частота останется неизменной.

   Несколько импульсов объединенных в группы с паузами определённой длины между ними называют пачками или пакетами. Генерируя разное число импульсов в группе и варьируя его, можно также передавать какую-либо информацию. 

   Для передачи информации в цифровой электронике можно использовать два и более проводников или каналов с разными импульсными сигналами. При этом информация передаётся с учётом определённых правил. Такой метод позволяет заметно увеличить скорость передачи информации или добавляет возможность управлением потоком информации между различными схемами. 

   Перечисленные возможности передачи информации с помощью импульсов могут быть использованы как сами по себе раздельно, так и в комбинации между собой. Существуют также множество стандартов передачи информации с помощью импульсов, например I2C, SPI, CAN, USB, LPT.

Широтно-Импульсная Модуляция — это способ кодирования аналогового сигналa путём изменения ширины (длительности) прямоугольных импульсов несущей частоты. 

Частота импульсов, а значит, и период T, остаются неизменными, при уменьшении ширины импульса t увеличивается пауза между импульсами (Б на Рис) и наоборот: при расширении импульса пауза сужается (В на Рис).

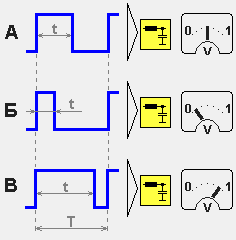
Зависимость напряжения от скважности ШИМ

   Если сигнал ШИМ пропустить через фильтр низших частот, то уровень постоянного напряжения на выходе фильтра будет определяться скважностью импульсов ШИМ. Назначение фильтра — не пропускать несущую частоту ШИМ. Сам фильтр может состоять из простейшей интегрирующей RC цепи, или же может отсутствовать вовсе, например, если оконечная нагрузка имеет достаточную инерцию. 

   Таким образом, имея в расположении лишь два логических уровня, «единицу» и «ноль», можно получить любое промежуточное значение аналогового сигнала. 

   Часто в схемах с ШИМ применяют обратную связь для управления длительностью импульса по той или иной закономерности, например, в схемах PID-регуляторов. 

   Простейшую схему ШИМ-управления можно собрать всего на нескольких транзисторах. Схема представляет собой одну из разновидностей генераторов импульсов — мультивибратор. Во время задающей цепи баз обоих транзисторов включён переменный резистор R6. Вращая его движок, можно в некоторых пределах регулировать скважность выходных импульсов. 

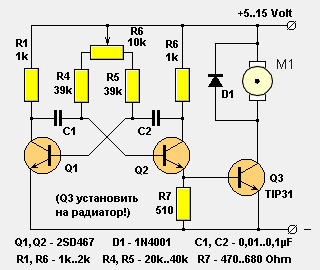
Мультивибратор с ШИМ

   Данная схема способна работать в широких пределах питающего напряжения от 5 до 15 вольт, можно использовать любые широко распространенные транзисторы и любой выпрямительный диод, номиналы сопротивлений могут отличаться на 10%.

В качестве нагрузки можно использовать любой мотор, насчитанный на то напряжение питания, которым питается вся схема.

Можно также подключить лампу накаливания и наблюдать изменение её яркости свечения, если подключить малогабаритный «динамик», то при вращении движка потенциометра можно услышать изменение характера звука. 

   Схемы простейших широтно-импульсных модуляторов можно построить и на логических элементах, и на микросхеме универсального таймера NE555 (отечественный аналог — КР1006ВИ1), и на операционном усилителе. Существуют и специально разработанные ШИМ-контроллеры. 

   В большинстве этих схем для изменения ширины выходного импульса так или иначе используется аналоговое напряжение. В цифровой же электронике для прямых операций с аналоговыми сигналами необходимо усложнять схему.

Поэтому схемы ШИМ-управления в цифровой технике строят на принципе отсчёта определённого числа импульсов задающего генератора.

Так, задавая количество отсчитываемых импульсов, можно точно отмерять длительность выходного импульса и паузы между импульсами. 

   На рисунке ниже приведен один из вариантов схемы с цифровой установкой ширины выходного импульса. Схема собрана на распространённых цифровых микросхемах серии К155 (зарубежный аналог — серия 74).

В качестве коммутирующего элемента P1 для эксперимента можно применить переключатель на 16 положений или просто подсоединять вход сброса RS-триггера к нужному выходу дешифратора.

В реальной же схеме можно применить микросхему селектор К155КП1 с соответствующей схемой цифрового управления. 

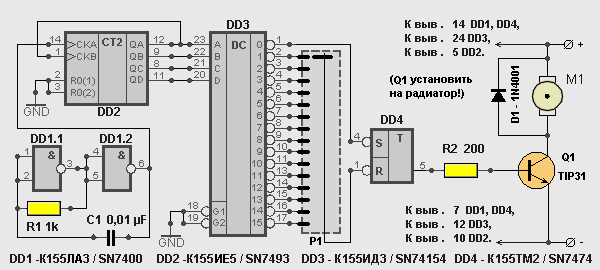
Цифровое формирование ШИМ

   В этой схеме применен четырёхразрядный двоичный счётчик К155ИЕ5. Максимальное число, которое можно представить, имея четыре разряда — 16. Поэтому в этой схеме частота выходных импульсов ШИМ будет в 16 раз ниже частоты счёта счётчика.

И таким же будет количество градаций регулировки ширины импульсов. При разработке цифровых устройств с ШИМ следует помнить, что чем больше разрядность ШИМ, тем больше градаций импульса можно получить и тем выше частота работы счётчика.

 

   Практически во всех современных микроконтроллерах имеются встроенные средства формирования одного или более независимых каналов ШИМ. Очень гибкие возможности конфигурации ШИМ-формирователя микроконтроллера позволяют использовать их в разнообразных схемах электронного управления и автоматики. 

   Пожалуй, наиболее часто ШИМ применяется для управления различными типами моторов. Тут основным достоинством ШИМ-управления является то, что электронный ключ (обычно транзистор) работает в ключевом режиме, что заметно повышает экономичность схемы, так как потери на активных элементах сводятся к минимуму. 

   Кроме того, широтно-импульсная модуляция применяется для формирования аналоговых сигналов сложной формы, в импульсных стабилизаторах, для кодирования и помехозащищённой передачи аналоговой информации. 

 Источник: https://www.myrobot.ru

Источник: https://www.autoscience.ru/blog/shirotno_impulsnaja_moduljacija_pulse_width_modulation/2013-12-18-44

Спектр периодической последовательности прямоугольных импульсов

• DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
• Распространяется под лицензией LGPL v3
• Страница проекта на GitHub.

Жан-Батист Жозеф Фурье 1768–1830 В предыдущих разделах мы рассмотрели разложение периодических сигналов в ряд Фурье, а также изучили некоторые свойства представления периодических сигналов рядом Фурье. Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент, отстоящих друг от друга на частоту рад/c, где  — период повторения сигнала. В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала. Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.

В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов, как одного из важнейших сигналов, используемого в практических приложениях.

Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , длительности секунд следующих с периодом секунд, как это показано на рисунке 1

Рисунок 1. Периодическая последовательность прямоугольных импульсов

Тогда спектр , , данного сигнала может быть представлен как:

(1)

Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида .

Свойства спектра периодической последовательности прямоугольных импульсов

Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.

Гийом Франсуа Лопиталь 1661–1704 Постоянная составляющая огибающей может быть получена как предел:

(2)

Для раскрытия неопределенности воспользуемся правилом Лопиталя [1, стр. 257]:

(3)

где называется скважностью импульсов и задает отношение периода повторения импульсов к длительности одиночного импульса.

Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность. При увеличении скважности (т.е. при уменьшении длительности импульса при фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.

Используя скважность импульсов выражение (1) можно переписать в виде:

1. (4)
2. Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:

где .

(5)

Знаменатель обращается в ноль только при , однако, как мы выяснили выше , тогда решением уравнения будет

(6)

Тогда огибающая обращается в ноль если

• (7)
• На рисунке 2 показана огибающая спектра периодической последовательности прямоугольных импульсов (пунктирная линия) и частотные соотношения огибающей и дискретного спектра .

Рисунок 2. Cпектр периодической последовательности прямоугольных импульсов

Также показаны амплитудная огибающая , амплитудный спектр , а также фазовая огибающая и фазовый спектр .

Из рисунка 2 можно заметить, что фазовый спектр принимает значения когда огибающая имеет отрицательные значения. Заметим, что и соответствуют одной и той же точке комплексной плоскости равной .

Пример спектра периодической последовательности прямоугольных импульсов

Пусть входной сигнал представляет собой периодическую последовательность прямоугольных импульсов амплитуды , следующих с периодом секунды и различной скважностью . На рисунке 3а показаны временные осциллограммы указанных сигналов, их амплитудные спектры (рисунок 3б), а также непрерывные огибающие спектров (пунктирная линия).

Рисунок 3. Cпектр периодической последовательности прямоугольных импульсов при различном значении скважностиа — временные осциллограммы; б — амплитудный спектр

Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов уменьшается, огибающая спектра расширяется и уменьшается по амплитуде (пунктирная линия). В результате, в пределах главного лепестка увеличивается количество гармоник спектра .

Спектр смещенной во времени периодической последовательности прямоугольных импульсов

Выше мы подробно изучили спектр периодической последовательности прямоугольных импульсов для случая, когда исходный сигнал являлся симметричным относительно . В результате спектр такого сигнала является вещественным и задается выражением (1). Теперь мы рассмотрим, что произойдет со спектром сигнала если мы сместим сигнал во времени,как это показано на рисунке 4 .

1. Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов
2. Смещенный сигнал можно представить как сигнал , задержанный на половину длительности импульса . Спектр смещенного сигнала можно представить согласно свойству циклического временного сдвига как:

(8)

Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не является чисто вещественной функцией, а приобретает дополнительный фазовый множитель . Амплитудный и фазовый спектры показаны на рисунке 5.

• Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической последовательности прямоугольных импульсов
• Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала, но добавляет линейную составляющую к фазовому спектру сигнала.

Выводы

1. В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.

2. Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры спектров при различном значении скважности.

3. Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано, что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.

Программная реализация в библиотеке DSPL

Данные для построения рисунков данного раздела были просчитаны при использовании библиотеки DSPL-2.0

Ниже приведён исходный код программы расчета данных для построения рисунка 3:

fourier_series_pimp_q.c #include #include #include «dspl.h» /* Размер векторов входных сигналов и огибающей спетра */ #define N 1000 /* Период повторения импульса. Для изменения скважности мы будем менять * длительность импульса при фиксированном периоде повторения */ #define T 4.0 /* Амплитуда */ #define A 2.0 /* Количество спектральных гармоник разложения в ряд Фурье */ #define M 41 /* длина команды Gnuplot */ #define PLOTCMD_LEN 256 int main(int argc, char* argv[]) { double t1[N]; /* время (сек) на одном периоде повторения */ double t4[N]; /* время (сек) на четырех периодах повторения */ double s[N]; /* входной сигнал */ complex_t S[M]; /* комплексный спектр периодического сигнала */ double Smag[M]; /* амплитудный спектр периодического сигнала */ double w[M]; /* частота (рад/c) дискретного спектра */ double wc[N]; /* частота (рад/с) огибающей спектра */ double Sc[N]; /* огибающая спектра */ double tau; /* длительность импульса */ /* скважность */ double Q[3] = {5.0, 2.0, 1.25}; int q, m, n; char fname[64]; /* имя файла данных */ char plotcmd[PLOTCMD_LEN]; /* Команда Gnuplot */ void* hdspl; /* DSPL handle */ void* hplot; /* GNUPLOT handle */ hdspl = dspl_load(); if(!hdspl) { printf(«Cannot to load libdspl!
«); return 0; } /* Вектор частот непрерывной огибаюхей вида sin(w/2*tau) / (w/2*T) */ linspace(-M_PI*(double)M/(double)T, M_PI*(double)M/(double)T, N, DSPL_SYMMETRIC, wc); /* заполнение массива временных отсчетов */ /* на одном периоде повторения сигнала */ linspace(-T/2.0, T/2.0, N, DSPL_PERIODIC, t1); /* заполнение массива временных отсчетов * на 4-x периодах повторения сигнала * для отображения на осциллограмме */ linspace(-T*2.0, T*2.0, N, DSPL_PERIODIC, t4); /* Построение графиков пакетом GNUPLOT */ gnuplot_create(argc, argv, 800, 640, «img/fourier_series_rec.png», &hplot); gnuplot_cmd(hplot, «unset key»); gnuplot_cmd(hplot, «set multiplot layout 3,2 rowsfirst»); gnuplot_cmd(hplot, «set yrange [0:2.2]»); for(q = 0; q < 3; q++) { tau = T/Q[q]; /* 4 периода повторения п-импульса скважности Q[q] */ signal_pimp(t4, N, A, tau, 0.0, T, s); /* сохранение в текстовый файл временных осциллограмм */ sprintf(fname, "dat/pimp_time_%.2lf.csv", Q[q]); writetxt(t4, s, N, fname); /* Построение временнОй осциллограммы */ sprintf(plotcmd, "plot '%s' with lines", fname); gnuplot_cmd(hplot, plotcmd); /* один период повторения п-импульса скважности Q[q] */ signal_pimp(t1, N, A, tau, 0.0, T, s); /* разложение в ряд Фурье */ fourier_series_dec(t1, s, N, T, M, w, S); /* Рассчет амплитудного спектра */ for(m = 0; m < M; m++) { /*printf("S[%d] = %f %f ", m, RE(S[m]), IM(S[m]));*/ Smag[m] = ABS(S[m]); } /* Сохранение в файл амплитудного спетра для скважности Q[q] */ sprintf(fname, "dat/pimp_freq_discrete_%.2lf.csv", Q[q]); writetxt(w, Smag, M, fname); /* Построение на график амплитудного спектра для заданной скважности */ sprintf(plotcmd, "plot '%s' with impulses lt 1 ,\", fname); printf("%s ", plotcmd); gnuplot_cmd(hplot, plotcmd); sprintf(plotcmd, "'%s' with points pt 7 ps 0.5 lt 1 ,\", fname); printf("%s ", plotcmd); gnuplot_cmd(hplot, plotcmd); /* Расчет огибающей */ for(n = 0; n < N; n++) Sc[n] = (wc[n] == 0.0) ? A/Q[q] : fabs( A * sin(0.5*wc[n]*tau) / (0.5*wc[n] * T)); /* сохранение огибающей в файл для скважности Q[q] */ sprintf(fname, "dat/pimp_freq_cont_%.2lf.csv", Q[q]); writetxt(wc, Sc, N, fname); /* Построение на график непрерывной огибающей амплитудного спектра для заданной скважности */ sprintf(plotcmd, "'%s' with lines", fname); printf("%s ", plotcmd); gnuplot_cmd(hplot, plotcmd); } gnuplot_cmd(hplot, "unset multiplot"); gnuplot_close(hplot); /* remember to free the resource */ dspl_free(hdspl); return 0; }

Смотри также

Представление периодических сигналов рядом Фурье Некоторые свойства разложения периодических сигналов в ряд Фурье Преобразование Фурье непериодических сигналов Свойства преобразования Фурье

Список литературы

[1] Ильин, В.А., Позняк Э.Г. Основы математического анализа. Москва, Наука, 1965, 572 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Гоноровский И.С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[4] Дёч, Г. Руководство по практическому применению преобразования Лапласа. Москва, Наука, 1965, 288 c.

[5] Bracewell, R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

© Бахурин Сергей 2015 — 2020. Все права защищены. Любое копирование материалов сайте без разрешения автора запрещено.

Источник: https://ru.dsplib.org/content/fourier_series_pimp/fourier_series_pimp.html