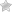Магнитная индукция: зависимость индуктивности в катушке от сердечника

• Факторы, влияющие на индуктивность катушки
• На индуктивность катушки оказывают влияние следующие основные факторы:
• Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.
• Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.
• 
• Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения — меньшую индуктивность.
• Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.
• 
• Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.
• Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.
• 
• Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника — тем меньше индуктивность.
• Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.
• 
• Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:
• 

Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.

Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр.

Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или  положением сердечника (который перемещается внутри катушки).

Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:

Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.

1. Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:
2. 
3. А это еще одна катушка индуктивности, так же предназначенная для радиостанций. Для большей жесткости ее провод намотан на керамический каркас:
4. 
5. Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:
6. 

Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L1 и L2. В непосредственной близости от них находятся резистор R3 и конденсатор С16. Показанные на плате катушки называются «торроидальными», так как их провод намотан вокруг сердечника, имеющего форму тора.

Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:

Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером «100», а над одной из них можно увидеть обозначение L5.

Источник: https://www.radiomexanik.spb.ru/14.-katushki-induktivnosti/3.-faktoryi-vliyayuschie-na-induktivnost-katushki.html

Катушки индуктивности и магнитные поля. Часть 2. Электромагнитная индукция и индуктивность

Взаимосвязь электрических и магнитных полей

Это открытие наводило на мысль о том, что из электрического тока можно получить магнитное поле. Но вместе с тем возникали мысли и по поводу обратного преобразования, а именно, как из магнитного поля получить электрический ток. Ведь многие процессы в природе обратимы: из воды получается лед, который можно снова растопить в воду.

На изучение этого очевидного сейчас закона физики после открытия Эрстеда ушло целых двадцать два года. Получением электричества из магнитного поля занимался английский ученый Майкл Фарадей.

Делались различной формы и размеров проводники и магниты, искались варианты их взаимного расположения. И только, видимо, случайно ученый обнаружил, что для получения на концах проводника ЭДС необходимо еще одно слагаемое – движение магнита, т.е.

магнитное поле должно быть обязательно переменным.

Сейчас это никого уже не удивляет. Именно так работают все электрические генераторы, — пока его чем-то вращают, электроэнергия вырабатывается, лампочка светит. Остановили, перестали вращать, и лампочка погасла.

Электромагнитная индукция

Таким образом, ЭДС на концах проводника возникает лишь в том случае, если его определенным образом перемещать в магнитном поле. Или, точнее говоря, магнитное поле обязательно должно изменяться, быть переменным.

Это явление получило название электромагнитной индукции, по-русски электромагнитное наведение: в этом случае говорят, что в проводнике наводится ЭДС.

Величина наведенной ЭДС зависит от нескольких факторов: длины проводника, индукции магнитного поля B, и в немалой степени от скорости перемещения проводника в магнитном поле. Чем быстрее вращать ротор генератора, тем напряжение на его выходе выше.

• Замечание: электромагнитную индукцию (явление возникновение ЭДС на концах проводника в переменном магнитном поле) не следует путать с магнитной индукцией – векторной физической величиной характеризующей собственно магнитное поле.
• Три способа получения ЭДС
• Индукция

Этот способ был рассмотрен в первой части статьи. Достаточно перемещать проводник в магнитном поле постоянного магнита, или наоборот перемещать (практически всегда вращением) магнит около проводника.

Оба варианта однозначно позволят получить переменное магнитное поле. В этом случае способ получения ЭДС называется индукцией. Именно индукция используется для получения ЭДС в различных генераторах.

В опытах Фарадея в 1831 году магнит поступательно перемещался внутри катушки провода.

Взаимоиндукция

Это название говорит о том, что в этом явлении принимают участие два проводника. В одном из них протекает изменяющийся ток, который создает вокруг него переменное магнитное поле. Если рядом находится еще один проводник, то на его концах возникает переменная же ЭДС.

Такой способ получения ЭДС называется взаимоиндукцией. Именно по принципу взаимоиндукции работают все трансформаторы, только проводники у них выполнены в виде катушек, а для усиления магнитной индукции применяются сердечники из ферромагнитных материалов.

Если ток в первом проводнике прекратится (обрыв цепи), или станет пусть даже очень сильным, но постоянным (нет никаких изменений), то на концах второго проводника никакой ЭДС получить не удастся. Вот почему трансформаторы работают только на переменном токе: если к первичной обмотке подключить гальваническую батарейку, то на выходе вторичной обмотки никакого напряжения однозначно не будет.

ЭДС во вторичной обмотке наводится только при изменении магнитного поля. Причем, чем сильнее скорость изменения, именно скорость, а не абсолютная величина, тем больше будет наведенная ЭДС.

Самоиндукция

Если убрать второй проводник, то магнитное поле в первом проводнике будет пронизывать не только окружающее пространство, но и сам проводник. Таким образом, под воздействием своего поля в проводнике наводится ЭДС, которая называется ЭДС самоиндукции.

Явления самоиндукции в 1833 году изучал русский ученый Ленц. На основании этих опытов удалось выяснить интересную закономерность: ЭДС самоиндукции всегда противодействует, компенсирует внешнее переменное магнитное поле, которое вызывает эту ЭДС. Эта зависимость называется правилом Ленца (не путать с законом Джоуля — Ленца).

Знак «минус» в формуле как раз и говорит о противодействии ЭДС самоиндукции причинам ее породившим. Если катушку подключить к источнику постоянного тока, ток будет возрастать достаточно медленно. Это очень заметно при «прозвонке» первичной обмотки трансформатора стрелочным омметром: скорость движения стрелки в сторону нулевого деления шкалы заметно меньше, чем при проверке резисторов.

При отключении катушки от источника тока ЭДС самоиндукции вызывает искрение контактов реле.

В случае, когда катушка управляется транзистором, например катушка реле, то параллельно ей ставится диод в обратном направлении по отношению к источнику питания.

Это делается для того, чтобы защитить полупроводниковые элементы от воздействия ЭДС самоиндукции, которая может в десятки и даже сотни раз превышать напряжение источника питания.

Для проведения опытов Ленц сконструировал интересный прибор. На концах алюминиевого коромысла закреплены два алюминиевых же кольца. Одно кольцо сплошное, а в другом был сделан пропил. Коромысло свободно вращалось на иголке.

При введении постоянного магнита в сплошное кольцо оно «убегало» от магнита, а при выведении магнита стремилось за ним. Те же самые действия с разрезанным кольцом никаких движений не вызывали.

Это объясняется тем, что в сплошном кольце под воздействием переменного магнитного поля возникает ток, который создает магнитное поле.

А в разомкнутом кольце тока нет, следовательно, нет и магнитного поля.

Немаловажная деталь этого опыта в том, что если магнит будет введен в кольцо и останется неподвижным, то никакой реакции алюминиевого кольца на присутствие магнита не наблюдается. Это лишний раз подтверждает, что ЭДС индукции возникает только в случае изменения магнитного поля, причем величина ЭДС зависит от скорости изменения. В данном случае просто от скорости перемещения магнита.

То же можно сказать и о взаимоиндукции и самоиндукции, только изменение напряженности магнитного поля, точнее скорость его изменения зависит от скорости изменения тока. Для иллюстрации этого явления можно привести такой пример.

Пусть через две достаточно большие одинаковые катушки проходят большие токи: через первую катушку 10А, а через вторую целых 1000, причем в обеих катушках токи линейно возрастают. Предположим, что за одну секунду ток в первой катушке изменился с 10 до 15А, а во второй с 1000 до 1001А, что вызвало появление ЭДС самоиндукции в обеих катушках.

Но, несмотря на такое огромное значение тока во второй катушке, ЭДС самоиндукции будет больше в первой, поскольку там скорость изменения тока 5А/сек, а во второй всего 1А/сек. Ведь ЭДС самоиндукции зависит от скорости возрастания тока (читай магнитного поля), а не от его абсолютной величины.

Индуктивность

Характеристика катушки, которая рассказывает об этом, называется коэффициентом индуктивности (самоиндукции) или просто индуктивностью. В формулах индуктивность обозначается буквой L, а на схемах этой же буквой обозначаются катушки индуктивности.

Единица измерения индуктивности – генри (Гн). Индуктивностью 1Гн обладает катушка, в которой при изменении тока на 1А в секунду вырабатывается ЭДС 1В. Это величина достаточно большая: индуктивностью в один и более Гн обладают сетевые обмотки достаточно мощных трансформаторов.

Поэтому достаточно часто пользуются величинами меньшего порядка, а именно милли и микро генри (мГн и мкГн). Такие катушки применяются в электронных схемах. Одно из применений катушек – колебательные контура в радиоустройствах.

Также катушки используются в качестве дросселей, основное назначение которых пропустить без потерь постоянный ток при этом ослабив переменный (фильтры в источниках питания). Как правило, чем выше рабочая частота, тем меньшей индуктивности требуются катушки.

Индуктивное сопротивление

Если взять достаточно мощный сетевой трансформатор и померить мультиметромсопротивление первичной обмотки, то окажется, что оно всего несколько Ом, и даже близко к нулю. Выходит, что ток через такую обмотку будет очень большим, и даже стремиться к бесконечности. Кажется, короткое замыкание просто неизбежно! Так почему же его нет?

Одним из основных свойств катушек индуктивности является индуктивное сопротивление, которое зависит от индуктивности и от частоты переменного тока, который подведен к катушке.

Нетрудно видеть, что с увеличением частоты и индуктивности индуктивное сопротивление увеличивается, а на постоянном токе вообще становится равным нулю. Поэтому при измерении сопротивления катушек мультиметром измеряется только активное сопротивление провода.

Конструкция катушек индуктивности весьма разнообразна и зависит от частот, на которых работает катушка. Например, для работы в дециметровом диапазоне радиоволн достаточно часто используются катушки, выполненные печатным монтажом. При массовом производстве такой способ очень удобен.

Индуктивность катушки зависит от ее геометрических размеров, сердечника, количества слоев и формы.

В настоящее время выпускается достаточное количество стандартных катушек индуктивности похожих на обычные резисторы с выводами. Маркировка таких катушек выполняется цветными кольцами.

Также существуют катушки для поверхностного монтажа, применяемые в качестве дросселей. Индуктивность таких катушек составляет несколько миллигенри.

Источник: https://www.alprof.info/articles/opisanie/katushki_induktivnosti_i_magnitnie_polia_chast_2_elektromagnitnaia_indukciia_i_induktivnost/

О сердечниках катушек индуктивности

Когда-то в среде «самодельщиков» телевизионных антенн циркулировали мифы о супер эффективности антенны с применением ртути, немного позднее жестяных пивных банок (правда неплохую антенну для Wi-Fi из пивной банки можно сделать, но не телевизионную).

Вероятно и по поводу сердечников существуют подобные мифы, тем более сами названия современных магнитных материалов (изоперм, пермендюр) внушают уверенность об их исключительной эффективности.

Рассмотрим вопрос применения магнитного сердечника в линейной сигнальной цепи, как он влияет на параметры катушки?

Итак, магнитный сердечник концентрирует магнитное поле и увеличивает индуктивность при тех же конструктивных параметрах катушки или позволяет уменьшить ее габариты при той же индуктивности.

Попробуем подобрать сердечник для фильтра акустической системы — crossover'а для экономии меди.

Сердечник должен иметь постоянные магнитные свойства до частот не менее 40 000 Гц при довольно больших токах намагничивания. Какой у нас выбор?

Современные магнитные материалы делятся на три группы:

• Металлические:
  1. Технически чистое железо (электротехническая малоуглеродистая сталь).
  2. Электротехнические кремнистые стали (трансформаторная сталь).
  3. Железоникелевые легированные кристаллические сплавы – пермаллой, суперпермаллой, муметалл, изоперм, пермендюр, перминвар, алфер, алфенол и т.д.
  4. Аморфные и нанокристаллические материалы – витровак, витроперм
• Порошковые материалы, магнитодиэлектрики — тонкие порошки карбонильного железа, пермаллоя или альсифера, смешанные с какой-либо диэлектрической связкой.
• Ферриты — керамические магнитные материалы.

Электротехническая малоуглеродистая сталь может применяться только в цепях постоянного тока, например реле, из-за недопустимо больших вихревых токов на переменном токе и больших потерь на перемагничивание.

Трансформаторная сталь немного лучше. Для уменьшения вихревых токов сердечник набирают из отдельных пластин. Однако выше 1000 Гц такой сердечник имеет недопустимые потери при больших токах намагничивания.

Железоникелевые сплавы имеют очень высокую начальную магнитную проницаемость, могут работать на частотах до 100 Кгц, но при этом у них малая индукция насыщения, т.е. они не могут работать в сильных полях. Зарекомендовали себя как незаменимый материал в магнитных головках магнитофонов, датчиках, магнитных экранах.

Аморфные и нанокристаллические материалы появились позднее чем пермаллои. У них шире частотный диапазон и немного выше индукция насыщения чем у пермаллоя, Применяются как трансформаторы тока в новых электросчетчиках, импульсные трансформаторы в БП, компенсированные дроссели и как более качественная замена пермаллоев.

Магнитодиэлектрики имеют широкий частотный диапазон до десятков мегагерц в зависимости от материала, но малую магнитную проницаемость и индукцию насыщения. Могут работать только в слабых полях. Применяются в технике ВЧ для изготовления магнитопроводов, сердечников катушек индуктивности и т. п

Ферриты обладают наименьшими потерями на вихревые токи и соответственно могут работать на самых высоких частотах из всех магнитных материалов. Однако имеют малую индукцию насыщения. Отличительной особенностью их является сильная зависимость параметров от температуры, а также старение материала, ухудшение его свойств со временем. Область применения каждой марки феррита определяется критической частотой, выше которой резко возрастают потери и снижается магнитная проницаемость.

Можно проследить общую тенденцию – при улучшении частотных параметров материала падает его индукция насыщения, т.е способность работать в сильных полях, а также магнитная проницаемость.

Самое главное, что любой магнитный материал меняет свои свойства в зависимости от частоты и силы намагничивающего поля.

А это значит, что катушка индуктивности с сердечником становится нелинейным элементом и вносит нелинейные искажения в проходящий через нее сигнал, особенно при большой индуктивности и силе тока. Ферриты, кроме того подвержены воздействию температуры.

Сердечники в виде стальных трубок, стержней из «супержелеза» вообще не имеют смысла, ну разве только в установках индукционного нагрева, там вихревые токи в сердечнике играют положительную роль. В цепях, где уровень сигнала слабый и сердечник далек от насыщения, решающий фактор — граничная частота сердечника.

При той же индуктивности сердечник даже увеличивает добротность катушки. В ВЧ дросселях потери в сердечнике играют положительную роль расширяя его частотный диапазон.Вывод: к подбору сердечника для индуктивности в сигнальной линейной цепи надо подходить взвешенно, учитывая как частотный диапазон, так и максимальный уровень сигнала, а также величину допустимых искажений.

Это не относится к импульсным сигналам и цепям, там все по другому…

Источник: https://coil32.ru/core.html

Трансформаторы,индуктивности,дроссели

(УПРОЩЕННЫЙ РАСЧЕТ)

       1. МАГНИТНЫЕ МАТЕРИАЛЫ И ИХ СВОЙСТВА    Из всего многообразия магнитных материалов остановимся на магнито-мягких ферритах, т.к. они способны работать в широком диапазоне как частот (от сотен Гц до сотен кГц), так и температур (от -60° С до +155° С не более).

Следует отметить, что на частотах — ниже 10 кГц габариты электромагнитных элементов оказываются завышенными, что и определяет ограничение применения.     

Ферриты имеют большое, удельное сопротивление, следовательно и пренебрежимо малые потери на вихревые токи. Однако потери на перемагничивании, связанные с «вязкостью» материала, значительны и достигают 3…5%. Поэтому КПД трансформаторов обычно лежит в пределах 0,95. ..0,97.

     Из последних разработок наиболее перспективными являются ферриты марок 2500НМС1 и 2500НМС2 как имеющие, в отличие от остальных марок, отрицательную температурную зависимость потерь. Применение феррита марки М2500НМС2 позволяет уменьшить массу на 8% и габариты на 15%, а при сохранении прежних типоразмеров — увеличить мощность на 20%.

Ферриты 2500НМС1 и 3000НМС обладают малыми значениями потерь в сильных магнитных полях в диапазоне частот, принятых в телевизионной технике, повышенной магнитной нндукцией при высоких температурах окружающей среды и при подмагничивании. Ферритовые сердечники используются, как правило, в относительно слабых магнитных полях напряженностью не более 10 А/см. В области средних полей (до Нт включительно) с ростом индукции растет и проницаемость, что обуславливает медленный рост потерь. При переходе в область сильных полей проницаемость начинает уменьшаться и уже не компенсирует рост индукции, вследствие чего потери резко возрастают. Из этого следует, что величина Вт и есть максимально допустимая индукция для любого феррита. Остаточная индукция Вг в сильных полях (свыше Вт) может составлять 0,3…0,6 индукции насыщения Bs.      Индукция насыщения, диапазон рабочих частот и температуры окружающей среды для некоторых марок феррита приведены в табл. 1. Точка Кюри выбираемого феррита должна превышать Максимальную рабочую температуру не менее чем на 30…40 0 С. Индукция Вт является максимально допустимой, т.к. переход в область более сильных полей приводит к резкому возрастанию потерь. На рис. 1 показана зависимость магнитной индукций для материала 2500НМС от напряженности и температуры. Аналогичная зависимость для материала 1500НМЗ показана на рис.2      Зависимость магнитной проницаемости от напряженности магнитного поля, вызванного подмагничиванием постоянным током, для разных материалов показана на рис.3 [1].      Влияние воздушного зазора на магнитную проницаемость показано на рис.4.      Напряженность магнитного поля трансформатора с подмагничнваинем постоянным током определяется:

•      Н = Iо*n/Lm, А/см (1)
•     Lm— эффективное значение длины средней силовой линии, см.                                                                       

     где Iо — сила постоянного тока, А;      n — число витков;

          2. ТИПОРАЗМЕРЫ СЕРДЕЧНИКОВ И ИХ ХАРАКТЕРИСТИКИ Из всего многообразия остановимся на трех основных типах: кольцевом, броневом и Ш-образном, которые показаны на рис.5…7. Осуществление миниатюризации источников вторичного электропитания (ИВЭП) идет по пути повышения частоты преобразования.

Это позволяет существенно уменьшить габариты моточ-ных изделий —трансформаторов и дросселей. Для этой цели наилучшим образом подходят кольцевые и броневые сердечники. Кольцевые сердечники имеют некоторое преимущество, т.к. имеют большее обмоточное пространство. Для трансформаторов с накоплением энергии (например ОНПШ, см.

ниже) и для дросселей с подмагничнваннем (PHI…PHIII) броневой сердечник предпочтительнее благодаря возможности создания немагнитного зазора.

Броневой сердечник является хорошим магнитным экраном для обмотки,находящейся внутри него, так как максимальное значение индукции Вт достигается лишь в центральном сечении, а в остальной части сердечника она мала.

При этом магнитные свойства феррита (в первую очередь магнитная проницаемость) достаточно высоки, поскольку сердечник имеет большой запас по объему магнитного материала. Благодаря этому сердечник имеет более мягкий переход от линейной области к области насыщения.

Иногда зазор выполняют не по всему сечению сердечника, что позволяет улучшить свойства феррита в более широком диапазоне нагрузок. Кроме того, сердечники этого типа удобно крепить на радиатор.

Кольцевой сердечник может создавать меньший уровень электромагнитного излучения по сравнению с броневым, но из-за несимметричной намотки может потребоваться его экранирование.  При выполнении трансформаторов и дросселей на кольцевых магнитопроводах обеспечивается наибольшая магнитная проницаемость, уменьшаются помехи и улучшаются электромагнитные свойства, т.к. магнитное поле заключено в пространстве, ограниченном обмотками. С ростом частоты преобразования растет и преимущество тороидальных сердечников. При одинаковых ампервитках индукция в кольцевых магнитопроводах больше, чем в броневых, что позволяет уменьшить массу и размеры трансформатора.

1. Ш-образные сердечники также уступают кольцевым, поскольку последние имеют лучшие теплоотводящие свойства благодаря большей поверхности охлаждения обмоток.
2. Броневые магннтопроводы применяются в случаях когда требуется:

• высокая добротность в заданной полосе;
• возможность регулировать индуктивность;
• обеспечение малого коэффициента вносимых нелинейных искажений;
• высокая устойчивость к механическим и климатическим воздействиям;
• отсутствие полей рассеяния.

• Основные геометрические параметры некоторых сердечников магнитопроводов приведены в табл. 2 [2], где: Sm — эффективное значение площади сечения магннтопровода; So — площадь окна магннтопровода;
• Vm = Lm*Sm — эффективный объем магннтопровода.

  3. ИНДУКТИВНОСТЬ Значения начальной индуктивности Al для некоторых типоразмеров магнитопроводов приведены в табл. 3.

Значения начальной индуктивности Al и эффективной магнитной проницаемости в зависимости от величины зазора для Ш-образных сердечников приведены в табл. 4.   Идуктйвность катушки равна   L = АL*n2 (2), откуда n=(L/AL)-2  (3).

Пример расчета 1: Сердечник Ml 500НМ К10x6x3 n = 300 L = ? Индуктивность катушки по формуле (2)

1. L = АL*n2= 440*ЗОО2 = 40 • 106 нГн = 40 мгн
2. L= 1840 *102 = 184*103нГн= 184мкГн.
3.   (4),

Пример расчета 2: Сердечник М2000НМ Ш7х7 n=10 L = ? Для любого другого магнитопровода^ не указанного в таблице, индуктивность катушки с ферромагнитным сердечником, у которой практически весь поток замыкается через сердечник, можно рассчитать по формуле: откуда n = 8920* где = 4*3,14*10-9 Гн/см — магнитная проницаемость вакуума;  — эффективное значение начальной магнитной проницаемости. Примечание При слабых переменных магнитных полях (Вm < 0,05 Тл) и отсутствии подмагничивания постоянным током эффективная магнитная проницаемость равна начальной, которая приводится справочниках для каждого типоразмера сердечника (для кольцевых магнитопроводов входит в марку феррита) и измеряется на частоте не более 10 кГц при напряженности поля Н не более 0,4 А/см. Из выражения следует, что индуктивность катушки при одном и том же числе витков зависит от отношения Sm/Lm, а так как с увеличением сердечника примерно в одинаковой степени растут как Sm, так и Lm, их отношение остается приблизительно постоянным. Поэтому при одном и том же числе витков индуктивности катушек, намотанных на маленьком и большом кольцах с одинаковой магнитной проницаемостью, примерно совпадают. Большое кольцо имеет преимущество в том случае, когда нужна большая добротность катушки. Граничная частота материала магнитопровода, начиная с которой необходимо секционирование обмоток:                              frp= 1000/, МГц. Пример расчета 3: Сердечник Ml 500НМ К10x6x3                                                                                                                                                             

• n = 300                                                                                                                                                                                                    
• L = 1,26 *10-8 *1500 *3002*0,06/2,45 = 0,04 Гн = 40 мГн.
• L = 1,26 • 10-8 *1490 *102 0,62/6,29 = 184 • 10-6Гн = 184 мкГн.

L = ? ‘ Индуктивность катушки по формуле (4) Пример расчета 4: Сердечник М2000НМ Ш7×7 n= 10 L = ? Как видно из примеров 1,3 и 2,4, результаты совпадают.

При увеличении амплитуды переменного тока эффективная магнитная проницаемость , а следовательно, и индуктивность катушки возрастают примерно в 1,5…2раза(взависимости от марки феррита и величины тока). С ростом же постоянной составляющей тока, , а следовательно, и индуктивность катушки, падают. Зависимость динамической магнитной проницаемости от подмагничивання показана на рис.8

Введение воздушного зазора эквивалентно параллельному включению индуктивности, обусловленной магнитным потоком в магиитопроводе (с нелинейной вебер-амперной характеристикой — рис.9, кривая 1), и потоком в зазоре (с линейной характеристикой — рис.9, кривая 2). Как показано на рис.9, кривая 3 — это наиболее эффективное приближение зависимости L(i) к линейной при работе с изменяющимся током подмагничивання. где— величина зазора, см. В любительских условиях это достигается разламыванием кольца на две части с последующим их склеиванием. Чаще всего индуктивности должны быть регулируемыми. Для этой цели больше всего подходят сердечники броневого типа. Начальная индуктивность в зависимости от величины зазора, типы подстроечных сердечников и коэффициент перекрытия (диапазон изменения индуктивности) для сердечников из материала 1500НМ приведены в табл.5.

Для получения стабильных во времени параметров индуктивностей сердечники подвергают старению (воздействию температуры на 10… 15° С выше верхней рабочей в течение 48 час), после чего катушки в сборе подвергают циклическому воздействию повышенной (+85°С) и пониженной (-60°С) температур — не менее пяти циклов.         

           4. ТРАНСФОРМАТОРЫ. ГАБАРИТНАЯ МОЩНОСТЬ МАГНИТОПРОВОДА    

Сердечник магнитопровода трансформатора выбирают исходя из необходимой габаритной мощности:где Pi =Ui* Ii — мощность i-ой обмотки. Как видим, габаритная мощность трансформатора равна полусумме мощностей всех обмоток (как первичных, так и вторичных). Обычно ее принимают равной сумме мощностей всех нагрузок.

Воспользуемся известной формулой для ЭДС индукции:  U = 4,44*f Bm*Sm *n*10-4 ,В (8) и выражением для тока обмотки:

 I = jSMKM102/2n , А (9),

где Км = Sn n/So = (0,1…0,35) — коэффициент заполнения окна медью;                                                                                  Sn — площадь поперечного сечения провода, мм2 ; n — число витков.

Перемножив U на I, получаем выражение для габаритной мощности: Ргаб = UI = 4,44f BmSmSo njKM10-2 /2n = 2,2SMSofBmjKM10-2, Bт (10) Поскольку диапазон изменения индукции при симметричном перемагничивании равен 2Вт, выражение (10) можно переписать в следующем виде: Ргаб = SmSo f jKm10-2 , Вт (11)  Из формулы следует, что при прочих равных условиях чем выше Км, тем выше коэффициент использования данного магнитопровода по мощности. С этой целью иногда используют провод прямоугольного сечения, а катушки выполняют бескаркасными, что позволяет довести Км до 0,7 против обычного 0,5. Кроме того, плоские провода имеют меньший поверхностный эффект (эффект вытеснения тока).  Для выбора магнитопровода удобно пользоваться произведением SoSm, характеризующим электромагнитную мощность:  (12), где — диапазон изменения магнитной индукции в сердечнике за время действия импульса tn. Тл (рис.10); = 2Bm

Источник: https://www.tor-trans.com.ua/transdrossely.html

Лабораторная работа № 32 определение индуктивности катушки Цель работы:

1. Ознакомиться с явлениями электромагнитной индукции и самоиндукции.

2. Определить индуктивность катушки методом амперметра и вольтметра.

3. Исследовать влияние ферромагнитного сердечника на индуктивность катушки.

Теоретическое введение

Магнитным потоком через бесконечно
малую площадкуdSназывается скалярная величина,
равная:

где B– индукция
магнитного поля, α – угол между вектором
магнитной индукции и нормальюк площадкеdS
(рис. 1). Магнитный потокΦ через
произвольную поверхностьSравен:

а в случае однородного поля и плоской
площадки:

Из
формулы (3) видно, что изменить магнитный
поток можно, изменяяВ, Sили α как по отдельности, так и вместе.

Рисунок 1 — Площадка dSв магнитном поле

В 1834 г.
М.

Фарадей открыл явление электромагнитной
индукции, заключающееся в следующем:
при любом изменении магнитного потока,
пронизывающего замкнутый проводящий
контур, в нём возникает ЭДС (ЭДС индукции)Εiи протекает
индукционный ток.

Согласнозакону
Фарадея(закону электромагнитной
индукции), ЭДС индукцииΕiсуществует только в те промежутки
времени, когда магнитный поток изменяется,
и равна (с обратным знаком) скорости
изменения магнитного потока:

где dΦ/dt– cкорость изменения магнитного потока.

Знак
минус показывает, что если Φ возрастает,
то естьdΦ/dt> 0, тоΕi< 0 и наоборот.

Этот знак выражаетправило Ленца, определяющее
направление индукционного тока:
индукционный ток имеет такое направление,
что своим магнитным полем противодействует
изменению магнитного потока, вызывающему
этот ток. Правило Ленца согласуется с
законом сохранения энергии.

• Электрический
  ток, текущий в замкнутом контуре (витке),
  создаёт вокруг себя магнитное поле,
  пронизывающее сам этот контур. Сцеплённый
  с контуром магнитный поток пропорционален
  силе тока, то есть:
• Φ ~ I(5)
• Отношение
  магнитного потока, сцеплённого с
  контуром, к силе тока, создающего этот
  магнитный поток, называется индуктивностью
  контура. Это – статическое определение
  индуктивности:
• L =
  . (6)
• Если
  контур состоит из Nвитков, намотанных на один каркас, то
  такой контур называют индуктивной
  катушкой и вводят понятиепотокосцепления
  Ψ:
• Ψ = Φ∙N , (7)
• где под Φ понимают магнитный поток
  через один виток. В этом случае
  индуктивность контура определяется
  соотношением:
• L =
  (8)
• Индуктивность
  измеряется в генри (Гн = Вб/А = В∙с/А =
  Ом∙с).
• Так как внутри
  катушки магнитное поле направлено вдоль
  её оси, то есть перпендикулярно плоскости
  витков, формула (3) принимает вид:
• Φ = B∙S. (9)
• Как известно,
  индукция магнитного поля связана с
  напряжённостью:
• В = μμоН , (10)
• где μ– магнитная проницаемость
  среды (сердечника, помещённого в катушку),μо = 4π∙10-7Гн/м – магнитная постоянная. Напряжённость
  магнитного поля внутри длинной катушки
  – соленоида (l >>d)
  равна:
• Н = I∙n, (11)
• где n = N/l– число витков на единицу длины,l– длина соленоида,d– его диаметр.
• Решая
  совместно (7), (8), (9), (10), (11) получим формулу
  для индуктивности длинного соленоида:
• L = μoμn2V
  ,(12)
• где V = l∙S
  = l∙πd2/4 – объём магнитного поля внутри
  соленоида.
• Если
  соленоид включить в цепь постоянного
  тока и измерить силу тока Iв цепи и напряжениеU,
  приложенное к соленоиду, то по закону
  Ома для постоянного тока можно найти
  сопротивлениеRпроволоки, из которой он изготовлен.
  Это сопротивление называетсяактивнымилиомическим:

При
включении соленоида в цепь переменного
тока магнитный поток, пронизывающий
витки катушки, изменяется. Это по закону
Фарадея приводит к возникновению в
катушке ЭДС индукции (в данном случае
называемой ЭДС самоиндукции) Εsi.

В результате возникаетиндукционный
ток, по правилу Ленца направленный
против «основного» тока в катушке, если
он («основной» ток) возрастает, и в том
же направлении, если он убывает. Таким
образом, при включении соленоида в цепь
переменного тока индукционный ток
препятствует возрастанию и убыванию
«основного» тока.

В результате в цепи
переменного тока сопротивление катушки
больше, чем в цепи постоянного тока, и
закон Ома для действующих значений токаIи напряженияUзаписывается
в виде:

где Z– полное
сопротивление цепи, определяемое
формулой:

Закон Фарадея
для ЭДС самоиндукции можно записать в
виде:

или, используя (8), Еsi
= —d(LI)/dt.
В случае, когдаLне
зависит от силы токаI,
формула ЭДС самоиндукции принимает
вид:

На основании
формулы (17) можно дать динамическое
определение индуктивности: величина,
равная модулю отношения ЭДС самоиндукции
Еsi,возникающей в контуре, к скорости
изменения силы токаdI/dtв нём, называется индуктивностью
контура:

Индуктивность
статическая равна динамической, если
она не зависит от силы тока. Это возможно,
если в катушке нет сердечника из
ферромагнитного материала.

При
наличии такого сердечника его магнитная
проницаемость μ является сложной
функцией напряжённости магнитного поляН(рис. 2), которая зависит от силы
токаI(см. формулу
(11)), и поэтому индуктивность является
сложной функциейI.

Рисунок 2 — Зависимость магнитной проницаемости μ ферромагнетика от напряжённости H магнитного поля (кривая Столетова)

Из формулы (15)
следует формула для расчёта индуктивности:

Источник: https://studfile.net/preview/3897791/

Индуктор: принцип работы, схема, ток и напряжение в нем

В данной статье мы подробно рассмотрим индуктор. Отдельно разберем индуктор на схеме, обратную ЭДС генерируемую индуктором, постоянную времени индуктора, ток и напряжение в индукторе, а так же мощность и энергию в индукторе.

Определение и принцип работы

В наших уроках об электромагнетизме мы увидели, что когда электрический ток протекает через проводник, вокруг проводника возникает магнитный поток.

 Это создает взаимосвязь между направлением магнитного потока, который циркулирует вокруг проводника, и направлением тока, протекающего через тот же проводник, что приводит к хорошо известной взаимосвязи между током и направлением магнитного потока, называемой «Правило правой руки Флеминга».

Но есть и другое важное свойство, относящееся к намотанной катушке, которая также существует, а именно то, что вторичное напряжение индуцируется в ту же катушку движением магнитного потока, поскольку оно противостоит любым изменениям электрического тока, протекающего по нему.

Типичный индуктор

В своей основной форме Индуктор — это не что иное, как катушка проволоки, намотанная вокруг центрального сердечника. Для большинства катушек ток I, протекающий через катушку, создает магнитный поток NΦ вокруг нее, который пропорционален этому потоку электрического тока.

Индуктор, называемый также дросселем, является еще одним типом пассивного электрического компонента, который является простой катушкой провода предназначенного, чтобы воспользоваться этой взаимосвязью путем индукции магнитного поля, сам по себе, или в активной зоне в результате тока, проходящем через катушки. Это приводит к гораздо более сильному магнитному полю, чем то, которое создавалось бы простой катушкой из проволоки.

Индукторы образованы проволокой, плотно обернутой вокруг сплошного центрального сердечника, который может представлять собой либо прямой цилиндрический стержень, либо непрерывную петлю или кольцо для концентрации их магнитного потока.

Схематическое обозначение индуктора — это катушка с проводом, поэтому катушку с проводом можно также назвать индуктором.

Индукторы обычно классифицируются в соответствии с типом внутреннего сердечника, вокруг которого они намотаны, например, полый сердечник, твердый железный сердечник или мягкий ферритовый сердечник, причем различные типы сердечников различаются путем добавления непрерывных или пунктирных параллельных линий рядом с проволочная катушкой, как показано ниже.

Индуктор на схеме

Ток I, который протекает через катушку индуктивности производит магнитный поток, который пропорционален к нему. Но в отличие от конденсатора, который противодействует изменению напряжения на своих пластинах, индуктор противодействует скорости изменения тока, протекающего через него, из-за накопления самоиндуцированной энергии в его магнитном поле.

Другими словами, катушки индуктивности сопротивляются или противостоят изменениям тока, но легко пропустят постоянный ток.

Поскольку Генри представляет собой относительно большую единицу индуктивности, для младших индукторов Генри используются для обозначения его значения. Например:

Префиксы индуктивности

Префикс	Условное обозначение	мультипликатор	Степень десяти
милли	m	1/1 000	10 -3
микро	μ	1/1000000	10 -6
нано	n	1/1000000000	10 -9

Таким образом, для отображения подразделов Генри мы будем использовать в качестве примера:

• 1mH = 1 милли-Генри   — что равно одной тысячной (1/1000) Генри.
• 100μH = 100 микро-Генри   — что равно одной 100-миллионной ( 1/1 000 000) Генри.

Индукторы или катушки очень распространены в электрических цепях, и существует множество факторов, определяющих индуктивность катушки, таких как форма катушки, число витков изолированного провода, число слоев провода, расстояние между витками, проницаемость материала сердечника, размер или площадь поперечного сечения сердечника и т. д.

Катушка индуктивности имеет площадь поперечного сечения сердечника ( A ) с постоянным числом витков провода на единицу длины ( l ).

Таким образом, если катушка N витков связана на величину магнитного потока Φ то катушка имеет потокосцепление NΦ и любой ток I, который протекает через катушку будет производить индуцированный магнитный поток в противоположном направлении по отношению к потоку тока. Затем, согласно закону Фарадея, любое изменение в этой связи магнитного потока производит самоиндуцированное напряжение в одной катушке:

Где:

•    N — число витков
•     А — площадь поперечного сечения в м 2
•    Φ — количество потока в Веберах
•     μ — проницаемость материала сердечника
•     L — длина катушки в метрах
•    di / dt — скорость изменения тока в Амперах в секунду

Изменяющееся во времени магнитное поле индуцирует напряжение, которое пропорционально скорости изменения тока, создающего его, с положительным значением, указывающим на увеличение ЭДС, и отрицательным значением, указывающим на уменьшение ЭДС. Уравнение, связывающее это напряжение, ток и индуктивность с самоиндукцией, может быть найдено путем замены μN 2 A / l на L, обозначая постоянную пропорциональности, называемую индуктивностью катушки.

Соотношение между потоком в катушке индуктивности и током, протекающим через катушку индуктивности, имеет вид: NΦ = Li . Поскольку катушка индуктивности состоит из катушки с проводящим проводом, это уменьшает приведенное выше уравнение, чтобы получить самоиндуцированную ЭДС, иногда называемую также обратной ЭДС, индуцированной в катушке.

Обратная ЭДС генерируемая индуктором

Где: L — собственная индуктивность, а 

di / dt — скорость изменения тока.

Таким образом, из этого уравнения мы можем сказать, что «самоиндуцированная ЭДС = индуктивность * скорость изменения тока» и цепь с индуктивностью один Генри будет иметь ЭДС 1 вольт, индуцированную в цепи, когда ток, протекающий через цепь, изменяется со скоростью 1 Ампер в секунду.

Катушка индуктивности

Один важный момент, который нужно отметить относительно приведенного выше уравнения. Он только связывает ЭДС, создаваемую через индуктор, с изменениями тока, потому что, если ток индуктора постоянен и не изменяется, например, в постоянном токе, то индуцированное напряжение ЭДС будет равно нулю, поскольку мгновенная скорость изменения тока равна ноль di / dt = 0.

При постоянном токе, протекающем через индуктор и, следовательно, нулевом индуцированном напряжении на нем, индуктор действует как короткое замыкание, равное куску провода, или, по крайней мере, очень низкое значение сопротивления. Другими словами, противодействие протеканию тока, предлагаемого индуктором, очень различно в цепях переменного и постоянного тока.

Постоянная времени индуктора

Теперь мы знаем, что ток не может изменяться мгновенно в индуктивности, потому что для этого ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной di / dt =  ∞ , делая индуцированную ЭДС бесконечной, а бесконечного напряжения не существует. Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.

Рассмотрим схему индуктора выше. Когда переключатель ( S1 ) разомкнут, ток через катушку индуктивности не течет.

Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю.

Если скорость изменения тока равна нулю, то  в катушке индуктивности нет ЭДС самоиндукции ( V L= 0 ).

Если мы теперь закроем переключатель (t = 0), ток будет проходить через цепь и медленно подниматься до своего максимального значения со скоростью, определяемой индуктивностью индуктора.

Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность по Генри, приводит к тому, что на катушке образуется некоторая самоиндуцированная ЭДС с фиксированным значением, определенная уравнением Фарадея V L  = Ldi / dt.

Эта самоиндуцированная ЭДС на катушке индуктивности ( V L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто устойчивое состояние.

Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.

Аналогичным образом, если переключатель ( S1 ) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается удержать ток в своем прежнем значении, индуцируя напряжение в другом направлении. Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.

Ток и напряжение в индукторе

Сколько индуктивного напряжения будет генерироваться индуктором, зависит от скорости изменения тока. В нашем уроке об электромагнитной индукции закон Ленца гласил: «Направление индуцированной ЭДС таково, что оно всегда будет противостоять изменению, которое его вызывает». Другими словами, индуцированная ЭДС всегда будет противопоставлять движение или изменение, которые изначально вызвали индуцированную ЭДС.

Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку, увеличение или уменьшение величины индуцированной ЭДС будет одинаковым.

Мощность в индукторе

Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца.

Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС.

Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V L), определяется как:

Мощность в цепи задается как P = V * I, поэтому:

Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.

Энергия в индукторе

Когда мощность поступает в индуктор, энергия накапливается в его магнитном поле. Когда ток, протекающий через индуктор, увеличивается и di / dt становится больше нуля, мгновенная мощность в цепи также должна быть больше нуля, ( P> 0 ), т.е. положительная, что означает, что энергия накапливается в индукторе.

Аналогичным образом, если ток через индуктор уменьшается и di / dt меньше нуля, то мгновенная мощность также должна быть меньше нуля ( P

Источник: https://meanders.ru/induktor.shtml