Формула индуктивного сопротивления катушки индуктивности: что это такое и от чего зависит

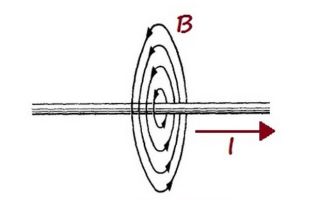
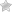Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением.

Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока.

Путем увеличения числа витков можно повысить индуктивность самой катушки.

Накопленная энергия в индуктивности

Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.

Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.

Гидравлическая модель

Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.

Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.

Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток  в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

• Добротность катушки индуктивности может быть найдена через следующую формулу:
•  где R является собственным сопротивлением обмотки.

Катушка индуктивности. Формула индуктивности

Базовая формула индуктивности катушки:

• L = индуктивность в генри
• μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
• μ г = относительная проницаемость материала сердечника
• N = число витков
• A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
• l = длина катушки в метрах (м)

Индуктивность прямого проводника:

• L = индуктивность в нГн
• l = длина проводника
• d = диаметр проводника в тех же единицах, что и l

Индуктивность катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = внешний радиус катушки
• l = длина катушки
• N = число витков

Индуктивность многослойной катушки с воздушным сердечником:

• L = индуктивность в мкГн
• r = средний радиус катушки
• l = длина катушки
• N = число витков
• d = глубина катушки

Индуктивность плоской катушки:

• L = индуктивность в мкГн
• r = средний радиус катушки
• N = число витков
• d = глубина катушки

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

1. Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
2. Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

• По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
• Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Источник: https://fornk.ru/1970-katushka-induktivnosti-opisanie-xarakteristiki-formula-rascheta/

Индуктивное реактивное сопротивление: формулы, схемы

В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.

Введение

Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.

Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .

Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения.

Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока.

Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи.

Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .

Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.

Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .

Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока.

 В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o .

 В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).

Схема индуктивности переменного тока

В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.

Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0о и 180о вдоль синусоиды.

Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.

Векторная диаграмма индуктора переменного тока

Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .

Мы можем также написать это заявление как, V L  = 0 ö и I L  = -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:

Где: ω в радианах в секунду, а 

t в секундах.

Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o .

 Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o .

 Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.

Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:

Где: ƒ — частота, L — индуктивность катушки и 

2πƒ = ω .

Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.

Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.

Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.

Индуктивное сопротивление от частоты

Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).

Питание от сети переменного тока серии LR

До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).

В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V R и V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V R и V L .

Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.

Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.

Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.

Цепь переменного тока серии LR

На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:

Треугольник сопротивления

В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.

Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».

Силовой треугольник индуктора переменного тока

Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник».

 Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах.

 В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .

В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания.

 Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью.

 Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.

Реактивная мощность ( Q ) катушки может быть задана как: I 2  x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.

Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.

Источник: https://meanders.ru/induktivnoe-soprotivlenie.shtml

Индуктивное сопротивление: обозначение, сопротивление катушки формула

Когда в цепи нарастает или уменьшается ток, электромагнитное поле создает противодействующую электродвижущую силу. Это явление порождается индуктивностью катушки. Индуктивное сопротивление воздействует только на переменный ток, быстрые изменения которого порождают противодействующую силу. В статье будет более подробно рассказано о природе этого явления.

Что зовется индуктивным сопротивлением

Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.

Схема для измерения

В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.

На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.

В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

Определение индуктивности

От каких факторов зависит сопротивление

Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.

Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.

В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.

Цепь, в которой возникает индукция

В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.

Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.

Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.

Принцип действия электродвижущей силы

Катушка индуктивности

Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.

Обычно каркас имеет цилиндрическую или тороидальную форму.

Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.

Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.

Катушки индуктивности

• Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
• Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
• Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.

Индуктивное сопротивление – единицы измерения

Измерение этой величины производится в омах. Здесь используются такая же единица измерения, как и для резистора, несмотря на то, что у них различная природа. Рассматриваемая величина порождается электродвижущей силой, противодействующей происходящему изменению. Обычное возникает в связи с рассеиванием энергии при прохождении электронов по проводнику.

Магнитное поле индуктивного элемента

Индуктивное сопротивление – как его найти

1. Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:
2. XL=2*П*v*L
3. Здесь употреблены следующие обозначения:

1. XL – рассматриваемая величина.

2. Символом «П» обозначено число Пи.
3. V представляет собой частоту.
4. L — это обозначение величины индуктивности.

Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».

Катушки с различными сердечниками

• Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:
• I = U / XL
• I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.

Конфигурация магнитного поля катушки

Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.

При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.

Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.

Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.

Магнитное поле провода

К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.

Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.

При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.

Источник: https://rusenergetics.ru/polezno-znat/induktivnoe-soprotivlenie

Индуктивное сопротивление катушки — Основы электроники

Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.

Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.

Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.

Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот.

Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки.

Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

 Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.

• Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
• Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
• XL=2π• f •L
• где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
• Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
• XL=ω•L

Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.

Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник: https://www.sxemotehnika.ru/induktivnoe-soprotivlenie-katushki.html

Формула индуктивного сопротивления

При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока.

В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока.

Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.

От чего зависит индуктивное сопротивление

Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.

Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.

Формула электрической мощности

Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.

На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов.

Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%.

Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.

Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.

Индуктивное сопротивление в цепи переменного тока

Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.

К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов.

Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным.

Длина каждого катета соответствует действующему значению того или иного сопротивления.

Применение электрического тока в металлах

В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока.

В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L).

Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.

Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени.

При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.

Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси).

Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности.

В результате, между током и напряжением происходит смещение фаз.

Индуктивное сопротивление катушки

Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.

Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля.

В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке.

Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.

Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.

Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.

Источник: https://electric-220.ru/news/formula_induktivnogo_soprotivlenija/2017-05-03-1254

Что такое катушка индуктивности и для чего она нужна?

Я получил письма от многих из вас с просьбой рассказать простыми словами о катушке индуктивности.

Это действительно хорошая просьба и желание). Потому что катушка индуктивности — это довольно странный компонент. Её невероятно легко сделать. Но немного сложнее понять как она работает.

Катушка индуктивности

Катушка индуктивности (иногда называют ее индуктором или дросселем) — это просто катушка проволоки, которая намотана вокруг какого-нибудь сердечника. Ядро сердечника может быть просто воздухом или магнитом.

Когда вы подаете ток через катушку, вокруг неё создается магнитное поле.

При использовании магнитного сердечника магнитное поле будет намного сильнее.

Как работает катушка индуктивности?

Ток через любой провод создаст магнитное поле. Катушка индуктивности имеет проволочную форму, поэтому магнитное поле будет намного сильнее.

Причина, по которой индуктор работает так, как он работает, заключается в этом магнитном поле. Отсюда вытекают и следующие свойства катушки.

Свойства катушки индуктивности:

• Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
• Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
• Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.

Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Более детально о принципе работы катушек индуктивности вы можете почитать на сайте.

Для чего вы можете использовать их?

Я почти никогда не использую катушки индуктивности. Главным образом потому, что я работаю в основном с цифровыми схемами. Но я использовал их иногда для создания фильтров, генераторов и блоков питания.

Вы часто найдете катушки индуктивности в аналоговой электронике переменного тока, такой как радиооборудование.

Источник: https://zen.yandex.ru/media/id/5d38230cd5135c00ad1384d4/5d613819ec575b00ad6dce12